
AllQuestion and Answers: Page 1832
Question Number 27447 Answers: 1 Comments: 0
Question Number 27446 Answers: 0 Comments: 3
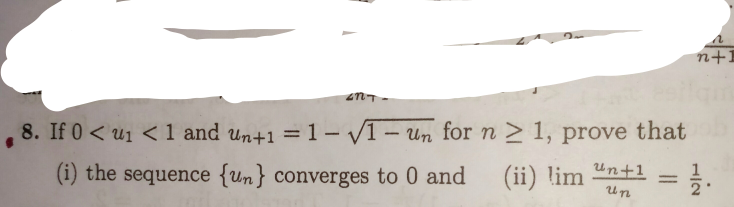
Question Number 27445 Answers: 1 Comments: 0
Question Number 27436 Answers: 1 Comments: 1
Question Number 27435 Answers: 1 Comments: 0
Question Number 27430 Answers: 0 Comments: 0
Question Number 27429 Answers: 1 Comments: 0

Question Number 27427 Answers: 0 Comments: 0
Question Number 27428 Answers: 0 Comments: 0
Question Number 27469 Answers: 1 Comments: 3

Question Number 27475 Answers: 0 Comments: 6

Question Number 27422 Answers: 0 Comments: 2
Question Number 27421 Answers: 1 Comments: 0
Question Number 27410 Answers: 0 Comments: 2
$$\underset{\mathrm{0}} {\overset{\infty} {\int}}\frac{{sinxdx}}{{x}} \\ $$
Question Number 27404 Answers: 1 Comments: 0
Question Number 27419 Answers: 1 Comments: 0
Question Number 27403 Answers: 1 Comments: 0
$${perimeter}\:{of}\:{a}\:{squre}\:\mathrm{112}{m}.{what}\:{is}\:{its}\:{area}.. \\ $$
Question Number 27402 Answers: 1 Comments: 0
Question Number 27400 Answers: 1 Comments: 4
$${Evaluate}\:\underset{{r}} {\overset{\mathrm{0}} {\int}}\sqrt{\frac{{x}}{{r}−{x}}}\:{dx} \\ $$
Question Number 27399 Answers: 1 Comments: 0
Question Number 27397 Answers: 2 Comments: 0
Question Number 27393 Answers: 1 Comments: 0
Question Number 27392 Answers: 0 Comments: 0
Question Number 27388 Answers: 0 Comments: 1
Question Number 27384 Answers: 1 Comments: 1
Question Number 27382 Answers: 1 Comments: 0
Pg 1827 Pg 1828 Pg 1829 Pg 1830 Pg 1831 Pg 1832 Pg 1833 Pg 1834 Pg 1835 Pg 1836
