Question and Answers Forum

AllQuestion and Answers: Page 1831

Question Number 27555 Answers: 0 Comments: 0

Question Number 27507 Answers: 1 Comments: 4

2(√(x ))+y=9....(1) x+ 2(√y)=3....(2) solve the simultaneous equation

$$\mathrm{2}\sqrt{{x}\:}+{y}=\mathrm{9}....\left(\mathrm{1}\right) \\ $$$${x}+\:\mathrm{2}\sqrt{{y}}=\mathrm{3}....\left(\mathrm{2}\right) \\ $$$$ \\ $$$${solve}\:{the}\:{simultaneous}\:{equation} \\ $$

Question Number 27503 Answers: 1 Comments: 0

If x=cy+bz ,y=az+cx & z=bx+ay prove that(x^2 /(1−a^2 ))=(y^2 /(1−b^2 ))=(z^2 /(1−c^2 )) .

$$\mathrm{If}\:\mathrm{x}=\mathrm{cy}+\mathrm{bz}\:,\mathrm{y}=\mathrm{az}+\mathrm{cx}\:\&\:\mathrm{z}=\mathrm{bx}+\mathrm{ay} \\ $$$$\mathrm{prove}\:\mathrm{that}\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{1}−\mathrm{a}^{\mathrm{2}} }=\frac{\mathrm{y}^{\mathrm{2}} }{\mathrm{1}−\mathrm{b}^{\mathrm{2}} }=\frac{\mathrm{z}^{\mathrm{2}} }{\mathrm{1}−\mathrm{c}^{\mathrm{2}} }\:. \\ $$

Question Number 27502 Answers: 0 Comments: 1

find ∫_0 ^(π/2) ((ln(1+xsin^2 t))/(sin^2 t))dt with −1<x<1 .

$${find}\:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\frac{{ln}\left(\mathrm{1}+{xsin}^{\mathrm{2}} {t}\right)}{{sin}^{\mathrm{2}} {t}}{dt}\:{with}\:−\mathrm{1}<{x}<\mathrm{1}\:. \\ $$

Question Number 27500 Answers: 0 Comments: 2

find ∫∫_Δ (√(4 −x^2 −y^2 )) dxdy with Δ={(x,y) ∈R^2 / x^2 +y^2 ≤2x}

$${find}\:\int\int_{\Delta} \sqrt{\mathrm{4}\:−{x}^{\mathrm{2}} −{y}^{\mathrm{2}} \:}\:\:{dxdy}\:{with} \\ $$$$\Delta=\left\{\left({x},{y}\right)\:\in\mathbb{R}^{\mathrm{2}} /\:{x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} \:\leqslant\mathrm{2}{x}\right\} \\ $$

Question Number 27498 Answers: 0 Comments: 0

find S_n = (C_n ^0 )^3 +( C_n ^1 )^3 +....(C_n ^n )^3 .

$${find}\:\:{S}_{{n}} \:=\:\:\left({C}_{{n}} ^{\mathrm{0}} \:\right)^{\mathrm{3}} \:\:+\left(\:{C}_{{n}} ^{\mathrm{1}} \right)^{\mathrm{3}} +....\left({C}_{{n}} ^{{n}} \right)^{\mathrm{3}} \:\:. \\ $$

Question Number 27497 Answers: 0 Comments: 0

let give I_n = n ∫_1 ^(1+(1/n)) f(x^n )dx with f is numerical function integrable on[1,e] .prove that lim_(n−>∝) I_n = ∫_1 ^e ((f(t))/t) dt.

$${let}\:{give}\:{I}_{{n}} =\:{n}\:\int_{\mathrm{1}} ^{\mathrm{1}+\frac{\mathrm{1}}{{n}}} {f}\left({x}^{{n}} \right){dx}\:{with}\:{f}\:{is}\:{numerical} \\ $$$${function}\:{integrable}\:{on}\left[\mathrm{1},{e}\right]\:.{prove}\:{that} \\ $$$${lim}_{{n}−>\propto} \:\:{I}_{{n}} \:=\:\int_{\mathrm{1}} ^{{e}} \:\:\frac{{f}\left({t}\right)}{{t}}\:{dt}. \\ $$

Question Number 27496 Answers: 0 Comments: 0

let give f(x)= ∫_0 ^∝ (1/(√t)) e^(−(1+ix)t) dt calculate f^′ (x) prove that ∃λ∈R/(x+i)^2 (f(x))^2 = λ then find ∫_0 ^∝ e^(−t^2 ) dt .

$${let}\:{give}\:{f}\left({x}\right)=\:\int_{\mathrm{0}} ^{\propto} \:\:\frac{\mathrm{1}}{\sqrt{{t}}}\:{e}^{−\left(\mathrm{1}+{ix}\right){t}} {dt} \\ $$$${calculate}\:{f}^{'} \left({x}\right)\:{prove}\:{that}\:\exists\lambda\in{R}/\left({x}+{i}\right)^{\mathrm{2}} \:\left({f}\left({x}\right)\right)^{\mathrm{2}} =\:\lambda \\ $$$${then}\:{find}\:\:\int_{\mathrm{0}} ^{\propto} \:\:{e}^{−{t}^{\mathrm{2}} } {dt}\:. \\ $$

Question Number 27495 Answers: 0 Comments: 1

find α and β from R /∫_0 ^π (αt^2 +βt)cos(nt)dt= (1/n^2 ) for all number n from N^(∗ ) then find Σ_(n=1) ^∝ (1/n^2 ) .

$${find}\:\alpha\:{and}\:\beta\:{from}\:{R}\:/\int_{\mathrm{0}} ^{\pi} \left(\alpha{t}^{\mathrm{2}} +\beta{t}\right){cos}\left({nt}\right){dt}=\:\frac{\mathrm{1}}{{n}^{\mathrm{2}} } \\ $$$${for}\:{all}\:{number}\:{n}\:{from}\:{N}^{\ast\:} \:{then}\:{find} \\ $$$$\sum_{{n}=\mathrm{1}} ^{\propto} \:\:\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\:. \\ $$

Question Number 27492 Answers: 0 Comments: 1

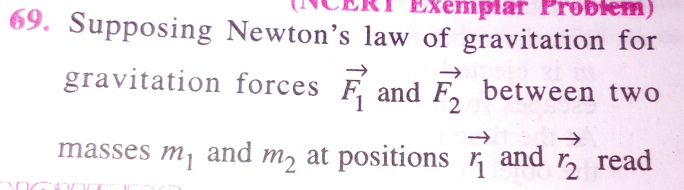
Question Number 27486 Answers: 0 Comments: 0

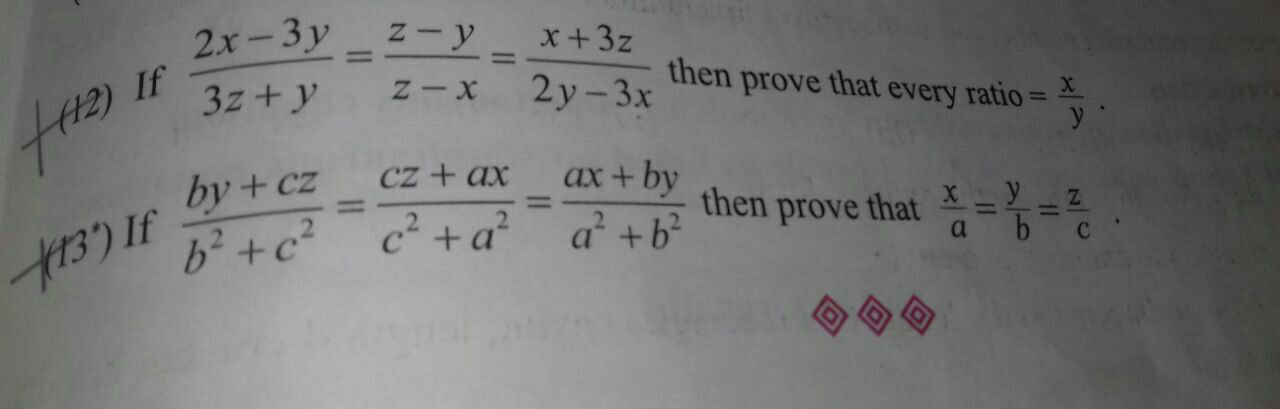
Question Number 27481 Answers: 0 Comments: 1

find the value of ∫_0 ^∝ ((√x)/(e^x −1))dx .

$${find}\:{the}\:{value}\:{of}\:\int_{\mathrm{0}} ^{\propto} \:\frac{\sqrt{{x}}}{{e}^{{x}} −\mathrm{1}}{dx}\:. \\ $$

Question Number 27467 Answers: 0 Comments: 0

Question Number 27464 Answers: 0 Comments: 5

Show that: ∫_( 0) ^( 2π) ((cos(3x))/(5 − 4cos(x))) dx = (π/(12))

$$\mathrm{Show}\:\mathrm{that}:\:\:\:\:\int_{\:\mathrm{0}} ^{\:\mathrm{2}\pi} \:\frac{\mathrm{cos}\left(\mathrm{3x}\right)}{\mathrm{5}\:−\:\mathrm{4cos}\left(\mathrm{x}\right)}\:\mathrm{dx}\:\:=\:\:\frac{\pi}{\mathrm{12}} \\ $$

Question Number 27449 Answers: 2 Comments: 0

factorise a^4 −(b+c)^4

$${factorise}\:{a}^{\mathrm{4}} −\left({b}+{c}\right)^{\mathrm{4}} \\ $$

Question Number 27447 Answers: 1 Comments: 0

∫^∞ _0 v^(4 ) e ((−mv^2 )/(2KT))dv solve it

$$\underset{\mathrm{0}} {\int}^{\infty} \:\mathrm{v}^{\mathrm{4}\:} \:\mathrm{e}\:\frac{−\mathrm{mv}^{\mathrm{2}} }{\mathrm{2KT}}\mathrm{dv}\: \\ $$$$\mathrm{solve}\:\mathrm{it} \\ $$

Question Number 27446 Answers: 0 Comments: 3

Question Number 27445 Answers: 1 Comments: 0

If a planet is suddenly stopped in its orbit, supposed to be circular, then it would fall into the sun in a time (T/(4(√2))), where T is the time period of revolution. Prove this.

$${If}\:{a}\:{planet}\:{is}\:{suddenly}\:{stopped}\:{in}\:{its} \\ $$$${orbit},\:{supposed}\:{to}\:{be}\:{circular},\:{then}\:{it} \\ $$$${would}\:{fall}\:{into}\:{the}\:{sun}\:{in}\:{a}\:{time}\:\frac{{T}}{\mathrm{4}\sqrt{\mathrm{2}}}, \\ $$$${where}\:{T}\:{is}\:{the}\:{time}\:{period}\:{of} \\ $$$${revolution}.\:{Prove}\:{this}. \\ $$

Question Number 27436 Answers: 1 Comments: 1

Car A is moving at a speed of 45km/h towards car B which is moving towards car A at a speed of 55km/h.If the two cars where initially seperated at a distance of 150m.Determine how long it will take the two cars to meet.

$${Car}\:{A}\:{is}\:{moving}\:{at}\:{a}\:{speed}\:{of}\: \\ $$$$\mathrm{45}{km}/{h}\:{towards}\:{car}\:{B}\:{which}\:{is} \\ $$$${moving}\:{towards}\:{car}\:{A}\:{at}\:{a}\:{speed}\: \\ $$$${of}\:\mathrm{55}{km}/{h}.{If}\:{the}\:{two}\:{cars}\:{where} \\ $$$${initially}\:{seperated}\:{at}\:{a}\:{distance} \\ $$$${of}\:\mathrm{150}{m}.{Determine}\:{how}\:{long}\:{it}\: \\ $$$${will}\:{take}\:{the}\:{two}\:{cars}\:{to}\:{meet}. \\ $$

Question Number 27435 Answers: 1 Comments: 0

An object has a constant acceleration a=4ms^(−2) .Its velocity is 1m/s at t=0,when it is at x=7m. How fast is it at x=8m?At what time is this?

$${An}\:{object}\:{has}\:{a}\:{constant} \\ $$$${acceleration}\:{a}=\mathrm{4}{ms}^{−\mathrm{2}} .{Its}\:{velocity} \\ $$$${is}\:\mathrm{1}{m}/{s}\:{at}\:{t}=\mathrm{0},{when}\:{it}\:{is}\:{at}\:{x}=\mathrm{7}{m}. \\ $$$${How}\:{fast}\:{is}\:{it}\:{at}\:{x}=\mathrm{8}{m}?{At}\:{what} \\ $$$${time}\:{is}\:{this}? \\ $$

Question Number 27430 Answers: 0 Comments: 0

A 2000kg space capsule is traveling away from the earth, determine the gravitational field strenght and gravitational force on the capsule due to the earth when it is (a) At a distance from the earth′s surface equal to the radius of the earth (b) At a very large distance away from the earth (Take g = 9.8Nkg^(−1) on earth surface)

$$\mathrm{A}\:\mathrm{2000kg}\:\mathrm{space}\:\mathrm{capsule}\:\mathrm{is}\:\mathrm{traveling}\:\mathrm{away}\:\mathrm{from}\:\mathrm{the}\:\mathrm{earth},\:\mathrm{determine}\:\mathrm{the} \\ $$$$\mathrm{gravitational}\:\mathrm{field}\:\mathrm{strenght}\:\mathrm{and}\:\mathrm{gravitational}\:\mathrm{force}\:\mathrm{on}\:\mathrm{the}\:\mathrm{capsule}\:\mathrm{due}\:\mathrm{to}\:\mathrm{the} \\ $$$$\mathrm{earth}\:\mathrm{when}\:\mathrm{it}\:\mathrm{is} \\ $$$$\left(\mathrm{a}\right)\:\mathrm{At}\:\mathrm{a}\:\mathrm{distance}\:\mathrm{from}\:\mathrm{the}\:\mathrm{earth}'\mathrm{s}\:\mathrm{surface}\:\mathrm{equal}\:\mathrm{to}\:\mathrm{the}\:\mathrm{radius}\:\mathrm{of}\:\mathrm{the}\:\mathrm{earth} \\ $$$$\left(\mathrm{b}\right)\:\mathrm{At}\:\mathrm{a}\:\mathrm{very}\:\mathrm{large}\:\mathrm{distance}\:\mathrm{away}\:\mathrm{from}\:\mathrm{the}\:\mathrm{earth}\:\left(\mathrm{Take}\:\:\mathrm{g}\:=\:\mathrm{9}.\mathrm{8Nkg}^{−\mathrm{1}} \:\mathrm{on}\right. \\ $$$$\left.\mathrm{earth}\:\mathrm{surface}\right) \\ $$

Question Number 27429 Answers: 1 Comments: 0

Question Number 27427 Answers: 0 Comments: 0

A particle of mass 2kg moves in a force field depending on a time t given by F = 24t^2 i + (36t − 16)j − 12tk assuming that at t = 0 the particle is located at r_0 = 3i − j + 4k and has v_0 = 6i + 5j − 8k. Find (a) Velocity at any time t (b) Position at any time t (c) τ (torgue) at any time t (d) Angular momentum at any time t above the Origin

$$\mathrm{A}\:\mathrm{particle}\:\mathrm{of}\:\mathrm{mass}\:\mathrm{2kg}\:\mathrm{moves}\:\mathrm{in}\:\mathrm{a}\:\mathrm{force}\:\mathrm{field}\:\mathrm{depending}\:\mathrm{on}\:\mathrm{a}\:\mathrm{time}\:\mathrm{t}\:\mathrm{given}\:\mathrm{by} \\ $$$$\mathrm{F}\:=\:\mathrm{24t}^{\mathrm{2}} \mathrm{i}\:+\:\left(\mathrm{36t}\:−\:\mathrm{16}\right)\mathrm{j}\:−\:\mathrm{12tk}\:\:\:\mathrm{assuming}\:\mathrm{that}\:\mathrm{at}\:\mathrm{t}\:=\:\mathrm{0}\:\mathrm{the}\:\mathrm{particle}\:\mathrm{is}\:\mathrm{located} \\ $$$$\mathrm{at}\:\:\mathrm{r}_{\mathrm{0}} \:=\:\mathrm{3i}\:−\:\mathrm{j}\:+\:\mathrm{4k}\:\:\mathrm{and}\:\:\mathrm{has}\:\:\:\mathrm{v}_{\mathrm{0}} \:=\:\mathrm{6i}\:+\:\mathrm{5j}\:−\:\mathrm{8k}.\:\mathrm{Find} \\ $$$$\left(\mathrm{a}\right)\:\mathrm{Velocity}\:\mathrm{at}\:\mathrm{any}\:\mathrm{time}\:\mathrm{t} \\ $$$$\left(\mathrm{b}\right)\:\mathrm{Position}\:\mathrm{at}\:\mathrm{any}\:\mathrm{time}\:\mathrm{t} \\ $$$$\left(\mathrm{c}\right)\:\tau\:\left(\mathrm{torgue}\right)\:\mathrm{at}\:\mathrm{any}\:\mathrm{time}\:\mathrm{t} \\ $$$$\left(\mathrm{d}\right)\:\mathrm{Angular}\:\mathrm{momentum}\:\mathrm{at}\:\mathrm{any}\:\mathrm{time}\:\mathrm{t}\:\mathrm{above}\:\mathrm{the}\:\mathrm{Origin} \\ $$

Question Number 27428 Answers: 0 Comments: 0

Find the workdone in moving an object along a vector r = 3i + 2j − 5k if the applied force is F = 2i − j − k

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{workdone}\:\mathrm{in}\:\mathrm{moving}\:\mathrm{an}\:\mathrm{object}\:\mathrm{along}\:\mathrm{a}\:\mathrm{vector} \\ $$$$\mathrm{r}\:=\:\mathrm{3i}\:+\:\mathrm{2j}\:−\:\mathrm{5k}\:\:\:\mathrm{if}\:\mathrm{the}\:\mathrm{applied}\:\mathrm{force}\:\mathrm{is}\:\:\mathrm{F}\:=\:\mathrm{2i}\:−\:\mathrm{j}\:−\:\mathrm{k} \\ $$

Question Number 27469 Answers: 1 Comments: 3

Question Number 27475 Answers: 0 Comments: 6

Pg 1826 Pg 1827 Pg 1828 Pg 1829 Pg 1830 Pg 1831 Pg 1832 Pg 1833 Pg 1834 Pg 1835

Contact: info@tinkutara.com