Question and Answers Forum

AllQuestion and Answers: Page 1829

Question Number 25955 Answers: 0 Comments: 0

find the value of ∫_0 ^∞ ln(2+x^2 )(1+x^2 )^(−1) dx

$$\boldsymbol{\mathrm{find}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{value}}\:\boldsymbol{\mathrm{of}}\:\int_{\mathrm{0}} ^{\infty} \:\:\boldsymbol{\mathrm{ln}}\left(\mathrm{2}+\boldsymbol{\mathrm{x}}^{\mathrm{2}} \right)\left(\mathrm{1}+\boldsymbol{\mathrm{x}}^{\mathrm{2}} \right)^{−\mathrm{1}} \boldsymbol{\mathrm{dx}} \\ $$

Question Number 25954 Answers: 0 Comments: 0

nswer to 25929 by binome formula (1+x)^(n+m) =Σ_(k=0) ^(k=n+m) C_(n+m) ^k x^k the coefficent of x^n is C_(n+m) ^n and the coefficient of x^m is C_(n+m) ^m but we have for p<n C_n ^p = C_n ^(n−p) >>>>>C_(n+m) ^n = C_(n+m) ^m .

$${nswer}\:{to}\:\mathrm{25929}\:\:\:{by}\:{binome}\:{formula}\:\:\: \\ $$$$\left(\mathrm{1}+{x}\right)^{{n}+{m}} \:\:=\sum_{{k}=\mathrm{0}} ^{{k}={n}+{m}} \:{C}_{{n}+{m}} ^{{k}} \:{x}^{{k}} \:\:\:\:{the}\:{coefficent}\:{of}\:{x}^{{n}} \:{is}\: \\ $$$${C}_{{n}+{m}} ^{{n}} \:{and}\:{the}\:{coefficient}\:{of}\:{x}^{{m}} \:\:{is}\:\:\:{C}_{{n}+{m}} ^{{m}} \:\:\:{but}\:{we}\:{have}\:\:{for} \\ $$$${p}<{n}\:\:\:\:{C}_{{n}} ^{{p}} \:\:\:=\:\:\:{C}_{{n}} ^{{n}−{p}} \:\:\:\:\:>>>>>{C}_{{n}+{m}} ^{{n}} \:\:=\:\:\:{C}_{{n}+{m}} ^{{m}} . \\ $$

Question Number 25949 Answers: 0 Comments: 0

Question Number 25948 Answers: 0 Comments: 1

Factorise: x^2 +y^2 −z^2 −2xy

$$\mathrm{Factorise}:\:\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} −{z}^{\mathrm{2}} −\mathrm{2}{xy} \\ $$

Question Number 25943 Answers: 1 Comments: 0

Question Number 26096 Answers: 0 Comments: 0

Question Number 25940 Answers: 0 Comments: 0

every extreme point is a critical point but every critical is not a extreme point justify it

$${every}\:{extreme}\:{point}\:{is}\:{a}\:{critical}\: \\ $$$${point}\:{but}\:{every}\:{critical}\:{is}\:{not}\:{a}\: \\ $$$${extreme}\:{point}\:{justify}\:{it}\: \\ $$

Question Number 25937 Answers: 1 Comments: 0

For a certain amount of work,Ade takes 6hours less than Bode.if they work together it takes them 13hours 20 minutes.How long will it take Bode alone to complete the work?

$${For}\:{a}\:{certain}\:{amount}\:{of}\:{work},{Ade}\:{takes} \\ $$$$\mathrm{6}{hours}\:{less}\:{than}\:{Bode}.{if}\:{they}\:{work}\:{together} \\ $$$${it}\:{takes}\:{them}\:\mathrm{13}{hours}\:\mathrm{20}\:{minutes}.{How} \\ $$$${long}\:{will}\:{it}\:{take}\:{Bode}\:{alone}\:{to}\:{complete} \\ $$$${the}\:{work}? \\ $$

Question Number 25934 Answers: 1 Comments: 2

Question Number 25932 Answers: 0 Comments: 0

answer to 25824 we have a^(−x^2 ) = e^(−x^2_ ln(a)) so for a>1 ln(a)=( (ln(a))^(1/2) )^2 >>>>∫_R a^(−^ x^2 ) = ∫_R e^(−(x (ln(a)^(1/2) )^2 ) dx and with the changement t=x (ln(a)^(1/2) >>>>x=t ( ln(a))^(−1/2) we have ∫_R a^(−x^2 ) dx = π^(1/2) (ln(a))^(−1/2) ...if 0<a<1 ln(a)<0 and the integrale is divergente...

$${answer}\:{to}\:\mathrm{25824}\:\:{we}\:{have}\:{a}^{−{x}^{\mathrm{2}} } \:=\:{e}^{−{x}^{\mathrm{2}_{} } {ln}\left({a}\right)} \:\:{so}\:{for}\:{a}>\mathrm{1} \\ $$$${ln}\left({a}\right)=\left(\:\left({ln}\left({a}\right)\right)^{\mathrm{1}/\mathrm{2}} \right)^{\mathrm{2}} >>>>\int_{{R}} {a}^{−^{} {x}^{\mathrm{2}} } \:=\:\int_{{R}} {e}^{−\left({x}\:\left({ln}\left({a}\right)^{\mathrm{1}/\mathrm{2}} \right)^{\mathrm{2}} \right.} {dx} \\ $$$${and}\:{with}\:{the}\:{changement}\:\:{t}={x}\:\left({ln}\left({a}\right)^{\mathrm{1}/\mathrm{2}} \:\:>>>>{x}={t}\:\left(\:{ln}\left({a}\right)\right)^{−\mathrm{1}/\mathrm{2}} \right. \\ $$$$\:{we}\:{have}\:\:\int_{{R}} {a}^{−{x}^{\mathrm{2}} } {dx}\:\:=\:\pi^{\mathrm{1}/\mathrm{2}} \left({ln}\left({a}\right)\right)^{−\mathrm{1}/\mathrm{2}} ...{if}\:\mathrm{0}<{a}<\mathrm{1}\:{ln}\left({a}\right)<\mathrm{0} \\ $$$$\:{and}\:{the}\:{integrale}\:{is}\:{divergente}... \\ $$

Question Number 25930 Answers: 2 Comments: 0

A line passes through A(−3, 0) and B(0, −4). A variable line perpendicular to AB is drawn to cut x and y-axes at M and N. Find the locus of the point of intersection of the lines AN and BM.

$$\mathrm{A}\:\mathrm{line}\:\mathrm{passes}\:\mathrm{through}\:{A}\left(−\mathrm{3},\:\mathrm{0}\right)\:\mathrm{and} \\ $$$${B}\left(\mathrm{0},\:−\mathrm{4}\right).\:\mathrm{A}\:\mathrm{variable}\:\mathrm{line}\:\mathrm{perpendicular} \\ $$$$\mathrm{to}\:{AB}\:\mathrm{is}\:\mathrm{drawn}\:\mathrm{to}\:\mathrm{cut}\:{x}\:\mathrm{and}\:{y}-\mathrm{axes}\:\mathrm{at} \\ $$$${M}\:\mathrm{and}\:{N}.\:\mathrm{Find}\:\mathrm{the}\:\mathrm{locus}\:\mathrm{of}\:\mathrm{the}\:\mathrm{point}\:\mathrm{of} \\ $$$$\mathrm{intersection}\:\mathrm{of}\:\mathrm{the}\:\mathrm{lines}\:{AN}\:\mathrm{and}\:{BM}. \\ $$

Question Number 25929 Answers: 0 Comments: 0

Show that the coefficients of x^m and x^n in (1+x)^(m+n) are equal.

$$\mathrm{Show}\:\mathrm{that}\:\mathrm{the}\:\:\mathrm{coefficients}\:\mathrm{of}\:\mathrm{x}^{\mathrm{m}} \:\mathrm{and}\:\mathrm{x}^{\mathrm{n}} \:\mathrm{in}\:\left(\mathrm{1}+\mathrm{x}\right)^{\mathrm{m}+\mathrm{n}} \mathrm{are}\:\mathrm{equal}. \\ $$

Question Number 25928 Answers: 0 Comments: 0

Expand (1−x)^4 .Hence,find S if S=(1−x^3 )^4 −4(1−x^3 )^3 +6(1−x^3 )^2 −4(1−x^3 )^ +1.

$$\mathrm{Expand}\:\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{4}} .\mathrm{H}\boldsymbol{\mathrm{ence}},\boldsymbol{\mathrm{find}}\:\boldsymbol{\mathrm{S}}\:\boldsymbol{\mathrm{if}}\:\boldsymbol{\mathrm{S}}=\left(\mathrm{1}−\mathrm{x}^{\mathrm{3}} \right)^{\mathrm{4}} −\mathrm{4}\left(\mathrm{1}−\mathrm{x}^{\mathrm{3}} \right)^{\mathrm{3}} +\mathrm{6}\left(\mathrm{1}−\mathrm{x}^{\mathrm{3}} \right)^{\mathrm{2}} −\mathrm{4}\left(\mathrm{1}−\mathrm{x}^{\mathrm{3}} \right)^{} +\mathrm{1}. \\ $$

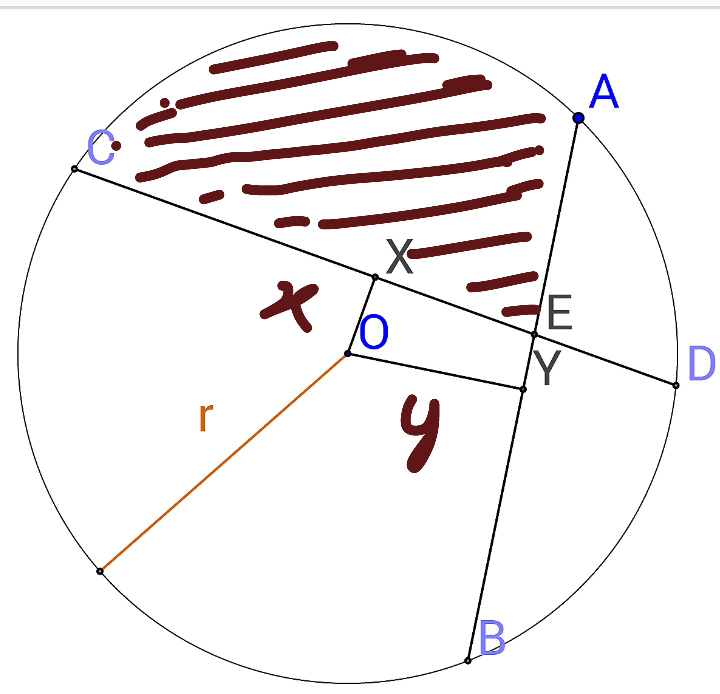
Question Number 25924 Answers: 1 Comments: 0

x+3+4=5

$${x}+\mathrm{3}+\mathrm{4}=\mathrm{5} \\ $$

Question Number 25899 Answers: 1 Comments: 1

8a^6 +5a^3 +1=factorize

$$\mathrm{8}{a}^{\mathrm{6}} +\mathrm{5}{a}^{\mathrm{3}} +\mathrm{1}={factorize} \\ $$

Question Number 25895 Answers: 1 Comments: 0

The hands of a clock have length 3cm and 5cm.Calculate the distance between the tips of the hand at 4 “0” clock.

$${The}\:{hands}\:{of}\:{a}\:{clock}\:{have}\:{length}\:\mathrm{3}{cm}\: \\ $$$${and}\:\mathrm{5}{cm}.{Calculate}\:{the}\:{distance}\:{between} \\ $$$${the}\:{tips}\:{of}\:{the}\:{hand}\:{at}\:\mathrm{4}\:``\mathrm{0}''\:{clock}. \\ $$

Question Number 25894 Answers: 0 Comments: 1

Question Number 25887 Answers: 1 Comments: 0

Question Number 25871 Answers: 0 Comments: 3

Question Number 25868 Answers: 0 Comments: 3

Question Number 25853 Answers: 0 Comments: 2

simplify: 3^x +4^x =5^x anybody to solve this

$${simplify}:\:\mathrm{3}^{{x}} +\mathrm{4}^{{x}} \:=\mathrm{5}^{{x}} \\ $$$${anybody}\:{to}\:{solve}\:{this} \\ $$

Question Number 25852 Answers: 0 Comments: 1

let s put H_n = 1 +2^(−1) +3^(−1) +....+n^(−1) and U_n = H_n −ln(n) prove that U_n is convergent to a number s wish verify 0<s<1 (s is named number of Euler )

$${let}\:{s}\:{put}\:{H}_{{n}} \:=\:\mathrm{1}\:+\mathrm{2}^{−\mathrm{1}} +\mathrm{3}^{−\mathrm{1}} +....+{n}^{−\mathrm{1}} \:{and}\:\:\:{U}_{{n}} =\:{H}_{{n}} \:−{ln}\left({n}\right) \\ $$$$\:{prove}\:{that}\:{U}_{{n}} \:{is}\:{convergent}\:{to}\:{a}\:{number}\:\:{s}\:{wish}\:{verify} \\ $$$$\mathrm{0}<{s}<\mathrm{1}\:\:\:\left({s}\:{is}\:{named}\:{number}\:{of}\:{Euler}\:\right) \\ $$

Question Number 25851 Answers: 0 Comments: 1

find the value of integral ∫_R (z−a)^(−1) dz with a from C aplly this result to find the value of ∫_0 ^∞ (2 +x^4_ )^(−1) dx.

$${find}\:{the}\:{value}\:{of}\:{integral}\:\:\:\int_{{R}} \left({z}−{a}\right)^{−\mathrm{1}} {dz}\:\:{with}\:{a}\:{from}\:{C}\:\:{aplly} \\ $$$${this}\:{result}\:{to}\:{find}\:{the}\:{value}\:{of}\:\:\:\int_{\mathrm{0}} ^{\infty} \left(\mathrm{2}\:+{x}^{\mathrm{4}_{} } \right)^{−\mathrm{1}} {dx}. \\ $$

Question Number 25865 Answers: 1 Comments: 0

∫((2+2x)/((x−1)(x^2 +1)))dx

$$\int\frac{\mathrm{2}+\mathrm{2}{x}}{\left({x}−\mathrm{1}\right)\left({x}^{\mathrm{2}} +\mathrm{1}\right)}{dx} \\ $$

Question Number 25846 Answers: 0 Comments: 3

determine the interval on which the given function is continuous f(x)= { ((sin (1/x)),(x≠0)),(x,(x=0)) :}

$${determine}\:{the}\:{interval}\:{on}\:{which}\:{the} \\ $$$${given}\:{function}\:{is}\:{continuous}\: \\ $$$${f}\left({x}\right)=\begin{cases}{\mathrm{sin}\:\frac{\mathrm{1}}{{x}}}&{{x}\neq\mathrm{0}}\\{{x}}&{{x}=\mathrm{0}}\end{cases} \\ $$

Question Number 25845 Answers: 2 Comments: 0

using the 1st principle find the derivative of y=(ax+b)^n

$${using}\:{the}\:\mathrm{1}{st}\:{principle}\:{find}\:{the} \\ $$$${derivative}\:{of}\: \\ $$$$\:\:\:\:\:{y}=\left({ax}+{b}\right)^{{n}} \\ $$

Pg 1824 Pg 1825 Pg 1826 Pg 1827 Pg 1828 Pg 1829 Pg 1830 Pg 1831 Pg 1832 Pg 1833

Contact: info@tinkutara.com