
AllQuestion and Answers: Page 1828
Question Number 28098 Answers: 1 Comments: 0
Question Number 28097 Answers: 0 Comments: 3
Question Number 28096 Answers: 0 Comments: 2
Question Number 28095 Answers: 0 Comments: 2
Question Number 28093 Answers: 0 Comments: 2
Question Number 28113 Answers: 1 Comments: 1
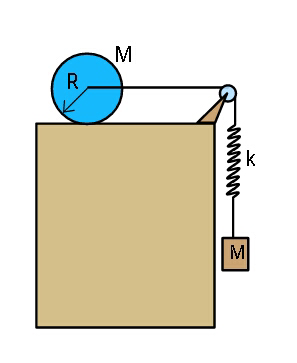
Question Number 28110 Answers: 0 Comments: 1

Question Number 28088 Answers: 0 Comments: 6
Question Number 28084 Answers: 0 Comments: 6
Question Number 28076 Answers: 1 Comments: 1
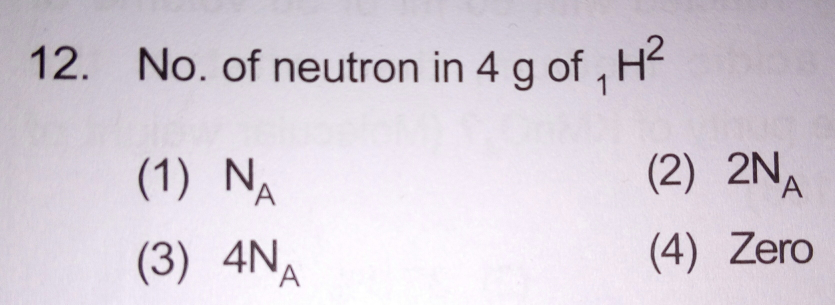
Question Number 28075 Answers: 0 Comments: 0

Question Number 28073 Answers: 0 Comments: 1
Question Number 28072 Answers: 0 Comments: 1
Question Number 28071 Answers: 0 Comments: 3
Question Number 28070 Answers: 1 Comments: 0

Question Number 28068 Answers: 0 Comments: 0
Question Number 28067 Answers: 0 Comments: 0
Question Number 28050 Answers: 0 Comments: 14

Question Number 28044 Answers: 0 Comments: 8

Question Number 28041 Answers: 0 Comments: 0
Question Number 28035 Answers: 0 Comments: 2
Question Number 28034 Answers: 0 Comments: 0
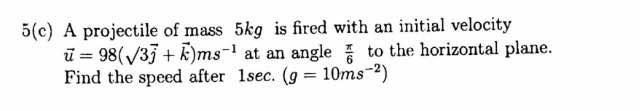
Question Number 28033 Answers: 0 Comments: 1
Question Number 28027 Answers: 1 Comments: 0
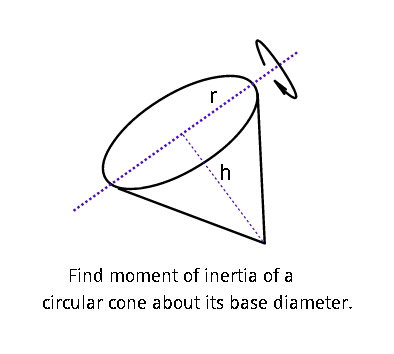
Question Number 36365 Answers: 1 Comments: 2

Question Number 36366 Answers: 3 Comments: 0

Pg 1823 Pg 1824 Pg 1825 Pg 1826 Pg 1827 Pg 1828 Pg 1829 Pg 1830 Pg 1831 Pg 1832
