
AllQuestion and Answers: Page 1827
Question Number 27912 Answers: 0 Comments: 2
Question Number 27797 Answers: 0 Comments: 1
$${find}\:\:\:\int\:\sqrt{\mathrm{2}+{tan}^{\mathrm{2}} {t}}\:\:{dt}. \\ $$
Question Number 27796 Answers: 0 Comments: 0
Question Number 27794 Answers: 0 Comments: 0
Question Number 27792 Answers: 0 Comments: 3
Question Number 27790 Answers: 0 Comments: 2
Question Number 27789 Answers: 0 Comments: 3
Question Number 27788 Answers: 0 Comments: 0
Question Number 27787 Answers: 1 Comments: 0
$${find}\:\:{lim}_{{x}−>\mathrm{0}} \frac{{e}^{{x}} \:\:−{x}−\mathrm{1}}{{x}^{\mathrm{2}} }\:. \\ $$
Question Number 27786 Answers: 0 Comments: 1
Question Number 27785 Answers: 0 Comments: 1
Question Number 27784 Answers: 0 Comments: 0
Question Number 27782 Answers: 0 Comments: 1
$${solve}\:{the}\:{e}.{d}.\:\:\:\:\:{xy}^{'} \:+\alpha{y}\:\:=\:{xe}^{−{x}} \:\:. \\ $$
Question Number 27781 Answers: 0 Comments: 1
Question Number 27774 Answers: 0 Comments: 1

Question Number 27771 Answers: 2 Comments: 1

Question Number 27769 Answers: 1 Comments: 0
Question Number 27767 Answers: 1 Comments: 0
Question Number 27764 Answers: 1 Comments: 0
Question Number 27761 Answers: 1 Comments: 0
Question Number 27729 Answers: 0 Comments: 0

Question Number 27727 Answers: 1 Comments: 0
Question Number 27723 Answers: 1 Comments: 0
Question Number 27722 Answers: 1 Comments: 0
Question Number 27718 Answers: 1 Comments: 0
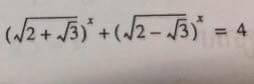
Question Number 27717 Answers: 0 Comments: 0

Pg 1822 Pg 1823 Pg 1824 Pg 1825 Pg 1826 Pg 1827 Pg 1828 Pg 1829 Pg 1830 Pg 1831
