Question and Answers Forum

All Questions Topic List

AllQuestion and Answers: Page 1826

Question Number 27614 Answers: 0 Comments: 2

∫((cosx)/(2−cosx))dx

$$\int\frac{{cosx}}{\mathrm{2}−{cosx}}{dx} \\ $$

Question Number 27613 Answers: 1 Comments: 1

find the value of ∫_0 ^∞ e^(−[x] −x) dx .

$${find}\:{the}\:{value}\:{of}\:\:\:\int_{\mathrm{0}} ^{\infty} \:\:{e}^{−\left[{x}\right]\:−{x}} {dx}\:\:. \\ $$

Question Number 27612 Answers: 1 Comments: 0

∫(1/(3+cos^2 x))dx

$$\int\frac{\mathrm{1}}{\mathrm{3}+{cos}^{\mathrm{2}} {x}}{dx} \\ $$

Question Number 27611 Answers: 1 Comments: 0

∫(1/(2sin^2 x + 4cos^2 x))dx

$$\int\frac{\mathrm{1}}{\mathrm{2sin}\:^{\mathrm{2}} {x}\:+\:\mathrm{4cos}\:^{\mathrm{2}} {x}}{dx} \\ $$

Question Number 27609 Answers: 0 Comments: 0

Δ=(√(m×φ)) Δ=mass gap m=mass φ=phi calculate phi to the same number of decimal places as the mass. use the mass of an electron

$$\Delta=\sqrt{{m}×\phi} \\ $$$$\Delta={mass}\:{gap} \\ $$$${m}={mass} \\ $$$$\phi={phi} \\ $$$${calculate}\:{phi}\:{to}\:{the}\:{same}\:{number}\:{of}\: \\ $$$${decimal}\:{places}\:{as}\:{the}\:{mass}. \\ $$$${use}\:{the}\:{mass}\:{of}\:{an}\:{electron} \\ $$

Question Number 27608 Answers: 0 Comments: 5

f(x) = ln(x +(√(x^2 +1))) find f^(−1) (x) plzz help

$$\mathrm{f}\left(\mathrm{x}\right)\:=\:\mathrm{ln}\left(\mathrm{x}\:+\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\right) \\ $$$$ \\ $$$$\mathrm{find}\:\mathrm{f}^{−\mathrm{1}} \left(\mathrm{x}\right) \\ $$$$\mathrm{plzz}\:\mathrm{help} \\ $$

Question Number 27607 Answers: 0 Comments: 0

Question Number 27606 Answers: 0 Comments: 0

Question Number 27605 Answers: 1 Comments: 0

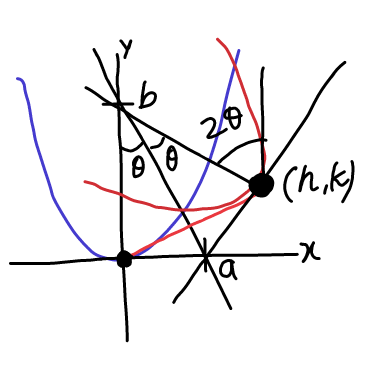
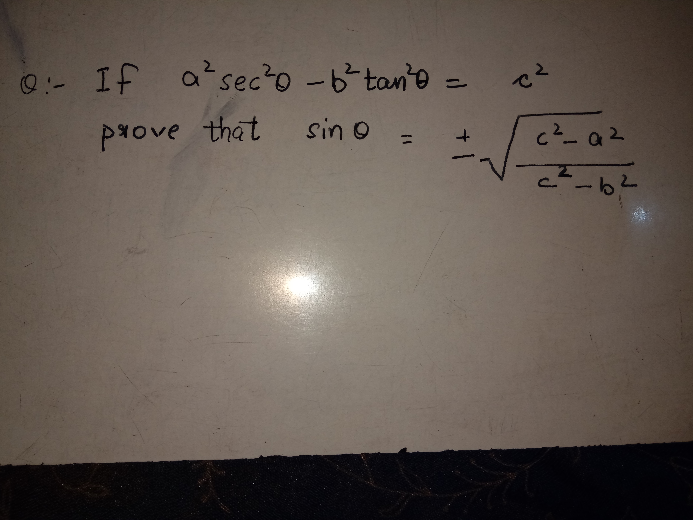
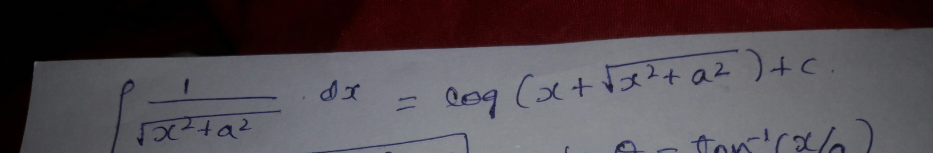
Question Number 27604 Answers: 0 Comments: 1

Let S_n =(1/1^3 ) + ((1+2)/(1^3 +2^3 )) +...+((1+2+...+n)/(1^3 +2^3 +...+n^3 )); n=1,2,3,.. Then S_n is greater than

$$\mathrm{Let}\: \\ $$$${S}_{{n}} =\frac{\mathrm{1}}{\mathrm{1}^{\mathrm{3}} }\:+\:\frac{\mathrm{1}+\mathrm{2}}{\mathrm{1}^{\mathrm{3}} +\mathrm{2}^{\mathrm{3}} }\:+...+\frac{\mathrm{1}+\mathrm{2}+...+{n}}{\mathrm{1}^{\mathrm{3}} +\mathrm{2}^{\mathrm{3}} +...+{n}^{\mathrm{3}} };\:{n}=\mathrm{1},\mathrm{2},\mathrm{3},.. \\ $$$$\mathrm{Then}\:{S}_{{n}} \:\mathrm{is}\:\mathrm{greater}\:\mathrm{than} \\ $$

Question Number 27601 Answers: 0 Comments: 0

f fonction numerical increasing on ]0,1] and ∫_0 ^1 f(t)dt converges prove that lim_(n−>∝) (1/n) Σ_(k=1) ^n f((k/n)) = ∫_0 ^1 f(t)dt .

$$\left.{f}\left.\:{fonction}\:{numerical}\:{increasing}\:{on}\:\right]\mathrm{0},\mathrm{1}\right]\:{and} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {f}\left({t}\right){dt}\:{converges}\:{prove}\:{that}\:\:{lim}_{{n}−>\propto} \:\:\frac{\mathrm{1}}{{n}}\:\sum_{{k}=\mathrm{1}} ^{{n}} \:{f}\left(\frac{{k}}{{n}}\right) \\ $$$$=\:\int_{\mathrm{0}} ^{\mathrm{1}} {f}\left({t}\right){dt}\:\:. \\ $$

Question Number 27600 Answers: 0 Comments: 1

find ∫_0 ^π (t/(2+sint)) dt

$${find}\:\:\:\int_{\mathrm{0}} ^{\pi} \:\:\frac{{t}}{\mathrm{2}+{sint}}\:{dt} \\ $$

Question Number 27599 Answers: 0 Comments: 0

let give the equation x^6 −x−1=0 by using Newton methodfind the approximate value of the real?root for this equation.

$${let}\:{give}\:{the}\:{equation}\:\:{x}^{\mathrm{6}} −{x}−\mathrm{1}=\mathrm{0}\:\:{by}\:{using}\:{Newton}\:{methodfind} \\ $$$${the}\:{approximate}\:{value}\:{of}\:{the}\:{real}?{root}\:\:{for}\:{this}\:{equation}. \\ $$

Question Number 27598 Answers: 0 Comments: 1

find ∫∫∫_D (x^2 +y^2 )dxdxy with D={x,y,z)∈R^3 /x^2 +y^2 +z^2 ≤1 and z≥0 }

$${find}\:\int\int\int_{{D}} \left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right){dxdxy}\:\:\:{with} \\ $$$$\left.{D}=\left\{{x},{y},{z}\right)\in{R}^{\mathrm{3}} \:\:\:/{x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} +{z}^{\mathrm{2}} \:\leqslant\mathrm{1}\:\:{and}\:{z}\geqslant\mathrm{0}\:\right\} \\ $$

Question Number 27597 Answers: 0 Comments: 0

find ∫ ((√(cos(2x)))/(cosx)) dx.

$${find}\:\int\:\:\frac{\sqrt{{cos}\left(\mathrm{2}{x}\right)}}{{cosx}}\:{dx}. \\ $$

Question Number 27596 Answers: 0 Comments: 1

find ∫ ^3 (√( x^2 −x^3 )) dx

$${find}\:\:\int\:\:\:^{\mathrm{3}} \sqrt{\:{x}^{\mathrm{2}} −{x}^{\mathrm{3}} }\:\:{dx} \\ $$

Question Number 27595 Answers: 0 Comments: 1

find ∫∫_D xy(√( x^2 +y^2 )) dxdy with D={ (x,y)∈R^2 / x^2 +2y^2 ≤1 ,x≥0 ,y ≥0}

$${find}\:\:\int\int_{{D}} \:\:{xy}\sqrt{\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\:\:{dxdy}\:\:\:{with} \\ $$$${D}=\left\{\:\left({x},{y}\right)\in{R}^{\mathrm{2}} /\:{x}^{\mathrm{2}} \:+\mathrm{2}{y}^{\mathrm{2}} \:\leqslant\mathrm{1}\:\:,{x}\geqslant\mathrm{0}\:,{y}\:\geqslant\mathrm{0}\right\} \\ $$

Question Number 27603 Answers: 0 Comments: 1

Find the value of i^i ?

$${Find}\:\:{the}\:{value}\:{of}\:\:\:{i}^{{i}} \:\:? \\ $$$$ \\ $$$$ \\ $$

Question Number 27587 Answers: 1 Comments: 1

divide 12x(8x−20) by 4(2x−5)

$$\mathrm{divide}\:\mathrm{12x}\left(\mathrm{8x}−\mathrm{20}\right)\:\mathrm{by}\:\mathrm{4}\left(\mathrm{2x}−\mathrm{5}\right) \\ $$

Question Number 27581 Answers: 1 Comments: 0

If f(x)=∫(4x−x^2 )dx f(3)=22, find f(x)

$$\mathrm{If}\:\boldsymbol{\mathrm{f}}\left(\boldsymbol{\mathrm{x}}\right)=\int\left(\mathrm{4}\boldsymbol{\mathrm{x}}−\boldsymbol{\mathrm{x}}^{\mathrm{2}} \right)\boldsymbol{\mathrm{dx}} \\ $$$$\mathrm{f}\left(\mathrm{3}\right)=\mathrm{22},\:\mathrm{find}\:{f}\left(\mathrm{x}\right) \\ $$

Question Number 27580 Answers: 1 Comments: 0

Simplify (1/(1−cos a)) + (1/(1+cos a)) and leave the answer in the form⇒ sin a

$$\mathrm{Simplify}\:\frac{\mathrm{1}}{\mathrm{1}−\mathrm{cos}\:\mathrm{a}}\:+\:\frac{\mathrm{1}}{\mathrm{1}+\mathrm{cos}\:\mathrm{a}} \\ $$$$\mathrm{and}\:\mathrm{leave}\:\mathrm{the}\:\mathrm{answer}\:\mathrm{in}\:\mathrm{the}\: \\ $$$$\mathrm{form}\Rightarrow\:\:\:\mathrm{sin}\:\mathrm{a} \\ $$

Question Number 27579 Answers: 1 Comments: 0

A circle with center (−3,1) passes through the point (3,1). Find it′s equation

$$\mathrm{A}\:\mathrm{circle}\:\mathrm{with}\:\mathrm{center}\:\left(−\mathrm{3},\mathrm{1}\right) \\ $$$$\mathrm{passes}\:\mathrm{through}\:\mathrm{the}\:\mathrm{point}\: \\ $$$$\left(\mathrm{3},\mathrm{1}\right).\:\mathrm{Find}\:\mathrm{it}'\mathrm{s}\:\mathrm{equation} \\ $$

Question Number 27578 Answers: 0 Comments: 1

if f(x)=((2x−3)/((x^2 −1)(x+2))) 1. Find the value for which f(x) is undefied. 2.Express f(x) in partial fraction

$$\mathrm{if}\:\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{2x}−\mathrm{3}}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)\left(\mathrm{x}+\mathrm{2}\right)} \\ $$$$\mathrm{1}.\:\mathrm{Find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{for}\:\mathrm{which}\:\mathrm{f}\left(\mathrm{x}\right)\:\mathrm{is}\:\mathrm{undefied}. \\ $$$$\mathrm{2}.\mathrm{Express}\:\mathrm{f}\left(\mathrm{x}\right)\:\mathrm{in}\:\mathrm{partial}\:\mathrm{fraction} \\ $$

Question Number 27577 Answers: 0 Comments: 0

find the equation of the line of the stationary point y=x^2 (x−3) and the distance between them

$$\mathrm{find}\:\mathrm{the}\:\mathrm{equation}\:\mathrm{of}\:\mathrm{the}\:\mathrm{line}\:\mathrm{of}\: \\ $$$$\mathrm{the}\:\mathrm{stationary}\:\mathrm{point}\: \\ $$$$\boldsymbol{\mathrm{y}}=\boldsymbol{\mathrm{x}}^{\mathrm{2}} \left(\boldsymbol{\mathrm{x}}−\mathrm{3}\right)\: \\ $$$$\mathrm{and}\:\mathrm{the}\:\mathrm{distance}\:\mathrm{between}\:\mathrm{them} \\ $$

Question Number 27594 Answers: 0 Comments: 1

solve the differencial equation (1−x^2 )y^′ −xy =1 .

$${solve}\:{the}\:\:{differencial}\:{equation} \\ $$$$\left(\mathrm{1}−{x}^{\mathrm{2}} \right){y}^{'} \:−{xy}\:=\mathrm{1}\:\:\:. \\ $$

Question Number 27568 Answers: 1 Comments: 0

carol is 6 times as old as her nephew Hondo.Baby is 22 years yonger than her aunt carol.In four years carol′s age will be twice the sum of Hondo′s and Baby′s age.How old is each perso n now?

$${carol}\:{is}\:\mathrm{6}\:{times}\:{as}\:{old}\:{as}\:{her}\:{nephew} \\ $$$${Hondo}.{Baby}\:{is}\:\mathrm{22}\:{years}\:{yonger}\:{than} \\ $$$${her}\:{aunt}\:{carol}.{In}\:{four}\:{years}\:{carol}'{s} \\ $$$${age}\:{will}\:{be}\:{twice}\:{the}\:{sum}\:{of}\:{Hondo}'{s} \\ $$$${and}\:{Baby}'{s}\:{age}.{How}\:{old}\:{is}\:{each}\:{perso} \\ $$$${n}\:{now}? \\ $$

Pg 1821 Pg 1822 Pg 1823 Pg 1824 Pg 1825 Pg 1826 Pg 1827 Pg 1828 Pg 1829 Pg 1830

Terms of Service

Contact: info@tinkutara.com