
AllQuestion and Answers: Page 1825
Question Number 28034 Answers: 0 Comments: 0
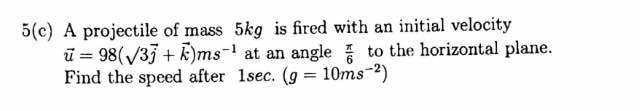
Question Number 28033 Answers: 0 Comments: 1
Question Number 28027 Answers: 1 Comments: 0
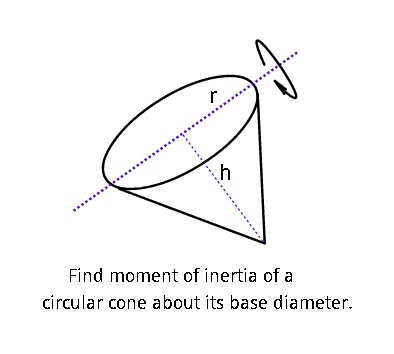
Question Number 36365 Answers: 1 Comments: 2

Question Number 36366 Answers: 3 Comments: 0

Question Number 28015 Answers: 1 Comments: 1

Question Number 28006 Answers: 0 Comments: 1
$$\int_{\mathrm{0}} ^{\infty} \left(\mathrm{ln}\:{x}\right)^{−\mathrm{3}} {dx} \\ $$
Question Number 27999 Answers: 0 Comments: 1
Question Number 27997 Answers: 1 Comments: 3
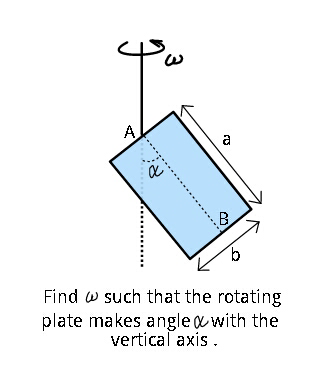
Question Number 27996 Answers: 1 Comments: 0
Question Number 27986 Answers: 0 Comments: 1
Question Number 27983 Answers: 2 Comments: 0
Question Number 28012 Answers: 1 Comments: 1
Question Number 27977 Answers: 1 Comments: 0
Question Number 27976 Answers: 1 Comments: 1
Question Number 27975 Answers: 1 Comments: 0
Question Number 27974 Answers: 0 Comments: 1
Question Number 27958 Answers: 1 Comments: 0
Question Number 27959 Answers: 0 Comments: 6

Question Number 27954 Answers: 0 Comments: 1

Question Number 27951 Answers: 0 Comments: 0
Question Number 27950 Answers: 0 Comments: 0
Question Number 27961 Answers: 0 Comments: 0
Question Number 27948 Answers: 0 Comments: 0
Question Number 27946 Answers: 1 Comments: 0
Question Number 27944 Answers: 0 Comments: 0
$${Did}\:{anybody}\:{give}\:{Silverzone}\:{iOM}\:{of} \\ $$$${class}\:\mathrm{11}? \\ $$
Pg 1820 Pg 1821 Pg 1822 Pg 1823 Pg 1824 Pg 1825 Pg 1826 Pg 1827 Pg 1828 Pg 1829
