
AllQuestion and Answers: Page 1824
Question Number 28435 Answers: 0 Comments: 0
Question Number 28434 Answers: 0 Comments: 0
Question Number 28433 Answers: 0 Comments: 0
Question Number 28432 Answers: 0 Comments: 1
Question Number 28431 Answers: 0 Comments: 0
Question Number 28430 Answers: 0 Comments: 1
Question Number 28429 Answers: 0 Comments: 1
Question Number 28428 Answers: 0 Comments: 1
Question Number 28427 Answers: 1 Comments: 1
Question Number 28426 Answers: 0 Comments: 0
Question Number 28417 Answers: 0 Comments: 0
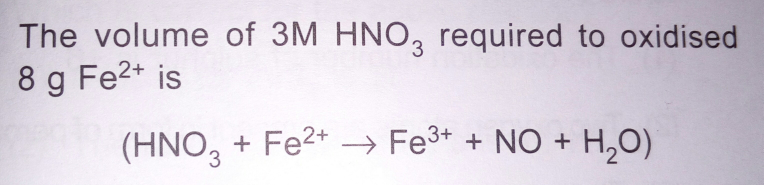
Question Number 28413 Answers: 0 Comments: 0
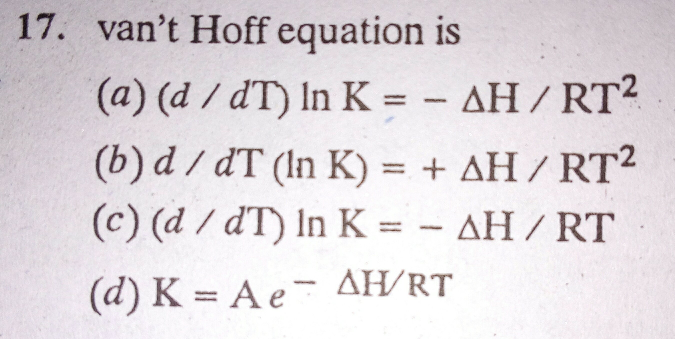
Question Number 28408 Answers: 0 Comments: 0
Question Number 28406 Answers: 1 Comments: 1
$${Image}\:{not}\:{getting}\:{attached}.\:{Please} \\ $$$${see}\:{the}\:{link}\:{below}. \\ $$
Question Number 28399 Answers: 1 Comments: 0

Question Number 28411 Answers: 2 Comments: 1

Question Number 28393 Answers: 0 Comments: 0
Question Number 28384 Answers: 2 Comments: 0

Question Number 28382 Answers: 1 Comments: 0
Question Number 28381 Answers: 0 Comments: 0

Question Number 28375 Answers: 1 Comments: 0
Question Number 28373 Answers: 1 Comments: 0
Question Number 28372 Answers: 0 Comments: 0
Question Number 28371 Answers: 0 Comments: 1
Question Number 28370 Answers: 0 Comments: 1
Question Number 28369 Answers: 0 Comments: 0
Pg 1819 Pg 1820 Pg 1821 Pg 1822 Pg 1823 Pg 1824 Pg 1825 Pg 1826 Pg 1827 Pg 1828
