
AllQuestion and Answers: Page 1823
Question Number 28169 Answers: 0 Comments: 1
Question Number 28168 Answers: 0 Comments: 0
Question Number 28166 Answers: 0 Comments: 0
Question Number 28165 Answers: 0 Comments: 0
Question Number 28164 Answers: 1 Comments: 0
Question Number 28163 Answers: 0 Comments: 0
Question Number 28162 Answers: 0 Comments: 1
Question Number 28161 Answers: 0 Comments: 0
Question Number 28160 Answers: 0 Comments: 2
Question Number 28159 Answers: 0 Comments: 1
Question Number 28158 Answers: 1 Comments: 0
Question Number 28185 Answers: 1 Comments: 0
Question Number 28151 Answers: 0 Comments: 4
Question Number 28139 Answers: 1 Comments: 0

Question Number 28138 Answers: 0 Comments: 1
Question Number 28202 Answers: 1 Comments: 1
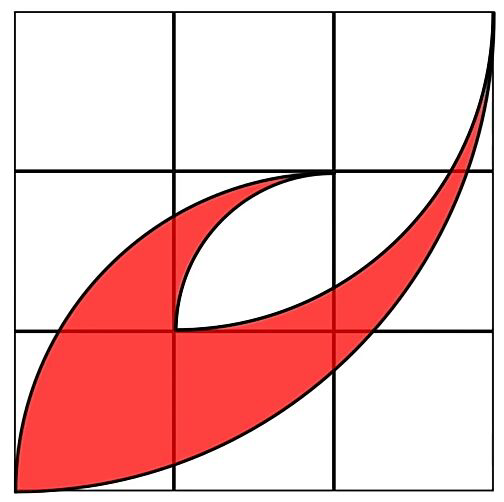
Question Number 28201 Answers: 0 Comments: 0
Question Number 28143 Answers: 1 Comments: 0
Question Number 28124 Answers: 0 Comments: 3
Question Number 28116 Answers: 0 Comments: 0

Question Number 28105 Answers: 0 Comments: 1

Question Number 28098 Answers: 1 Comments: 0
Question Number 28097 Answers: 0 Comments: 3
Question Number 28096 Answers: 0 Comments: 2
Question Number 28095 Answers: 0 Comments: 2
Question Number 28093 Answers: 0 Comments: 2
Pg 1818 Pg 1819 Pg 1820 Pg 1821 Pg 1822 Pg 1823 Pg 1824 Pg 1825 Pg 1826 Pg 1827
