
AllQuestion and Answers: Page 1822
Question Number 28288 Answers: 2 Comments: 0
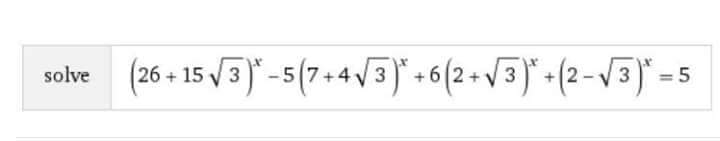
Question Number 28285 Answers: 0 Comments: 1
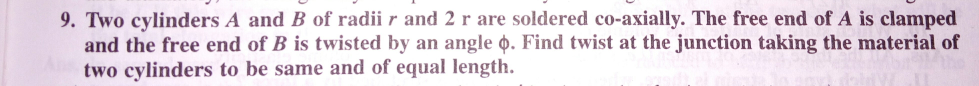
Question Number 28280 Answers: 1 Comments: 4
Question Number 28278 Answers: 2 Comments: 1

Question Number 28275 Answers: 0 Comments: 2
Question Number 28268 Answers: 0 Comments: 1
Question Number 28267 Answers: 1 Comments: 1
Question Number 28265 Answers: 0 Comments: 0
Question Number 28264 Answers: 0 Comments: 0
Question Number 28263 Answers: 0 Comments: 0
Question Number 28262 Answers: 0 Comments: 1
$${find}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dx}}{\mathrm{1}+{x}^{\mathrm{5}} }\:. \\ $$
Question Number 28261 Answers: 0 Comments: 0
Question Number 28260 Answers: 0 Comments: 0
Question Number 28259 Answers: 0 Comments: 0
Question Number 28258 Answers: 0 Comments: 1
Question Number 28257 Answers: 0 Comments: 0
Question Number 28248 Answers: 1 Comments: 0

Question Number 28247 Answers: 0 Comments: 1
Question Number 28242 Answers: 0 Comments: 1
$${find}\:{the}\:{value}\:{of}\:\int_{\mathrm{0}} ^{\infty} {e}^{−{x}} {lnxdx}\:\:. \\ $$
Question Number 28241 Answers: 1 Comments: 1

Question Number 28240 Answers: 1 Comments: 0

Question Number 28255 Answers: 0 Comments: 0
Question Number 28256 Answers: 0 Comments: 0
Question Number 28219 Answers: 0 Comments: 4

Question Number 28211 Answers: 0 Comments: 6

Question Number 28199 Answers: 1 Comments: 0
Pg 1817 Pg 1818 Pg 1819 Pg 1820 Pg 1821 Pg 1822 Pg 1823 Pg 1824 Pg 1825 Pg 1826
