Question and Answers Forum

AllQuestion and Answers: Page 1819

Question Number 28616 Answers: 0 Comments: 0

let give u_n = (1+(1/n))^n −e find nature of Σ u_n .

$${let}\:{give}\:{u}_{{n}} =\:\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)^{{n}} \:−{e}\:\:\:{find}\:{nature}\:{of}\:\:\Sigma\:{u}_{{n}} . \\ $$

Question Number 28615 Answers: 0 Comments: 0

find ∫_0 ^∞ ((shx)/x) e^(−3x) dx .

$${find}\:\:\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{shx}}{{x}}\:{e}^{−\mathrm{3}{x}} {dx}\:. \\ $$

Question Number 28614 Answers: 0 Comments: 2

find Σ_(n=1) ^∞ ((sin(nx))/n).

$${find}\:\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{{sin}\left({nx}\right)}{{n}}. \\ $$$$ \\ $$

Question Number 28613 Answers: 0 Comments: 1

let give x>0 and S(x)= ∫_0 ^∞ ((sint)/(e^(xt) −1))dt . developp S at form of series.

$${let}\:{give}\:{x}>\mathrm{0}\:\:{and}\:{S}\left({x}\right)=\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{sint}}{{e}^{{xt}} −\mathrm{1}}{dt}\:. \\ $$$${developp}\:{S}\:{at}\:{form}\:{of}\:{series}. \\ $$

Question Number 28612 Answers: 0 Comments: 0

let give u_(n ) = Σ_(k=1) ^n ((sin(kα))/(n+k)) and α∈R find lim _(n→+∞) u_n .

$${let}\:{give}\:\:{u}_{{n}\:} =\:\sum_{{k}=\mathrm{1}} ^{{n}} \:\:\frac{{sin}\left({k}\alpha\right)}{{n}+{k}}\:{and}\:\:\alpha\in{R} \\ $$$${find}\:{lim}\:_{{n}\rightarrow+\infty} {u}_{{n}} \:\:. \\ $$

Question Number 28610 Answers: 0 Comments: 0

let give I(x)= ∫_0 ^(π/2) (dt/(√(sin^2 t +x^2 cos^2 t))) and J(x)= ∫_0 ^(π/2) ((cost)/(√(sin^2 t +x^2 cos^2 t)))dt cslculate lim_(x→0^+ ) (I(x)−J(x)) and prove that I(x)=_(x→0^+ ) −lnx +2ln2 +o(1).

$${let}\:{give}\:{I}\left({x}\right)=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\frac{{dt}}{\sqrt{{sin}^{\mathrm{2}} {t}\:+{x}^{\mathrm{2}} \:{cos}^{\mathrm{2}} {t}}}\:\:{and} \\ $$$${J}\left({x}\right)=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\frac{{cost}}{\sqrt{{sin}^{\mathrm{2}} {t}\:+{x}^{\mathrm{2}} {cos}^{\mathrm{2}} {t}}}{dt}\:{cslculate}\:{lim}_{{x}\rightarrow\mathrm{0}^{+} } \left({I}\left({x}\right)−{J}\left({x}\right)\right) \\ $$$${and}\:{prove}\:{that}\:\:{I}\left({x}\right)=_{{x}\rightarrow\mathrm{0}^{+} } \:−{lnx}\:+\mathrm{2}{ln}\mathrm{2}\:+{o}\left(\mathrm{1}\right). \\ $$

Question Number 28609 Answers: 0 Comments: 0

calculate cotanx −2cotan(2x)then simlify Σ_(k=0) ^n (1/2^k )tan((α/2^k )).

$${calculate}\:{cotanx}\:−\mathrm{2}{cotan}\left(\mathrm{2}{x}\right){then}\:{simlify} \\ $$$$\sum_{{k}=\mathrm{0}} ^{{n}} \:\:\frac{\mathrm{1}}{\mathrm{2}^{{k}} }{tan}\left(\frac{\alpha}{\mathrm{2}^{{k}} }\right). \\ $$$$ \\ $$

Question Number 28608 Answers: 1 Comments: 0

transform tanp−tanq then find the value of Σ_(k=1) ^n (1/(cos(kθ)cos((k+1)θ)) . θ∈R.

$${transform}\:{tanp}−{tanq}\:{then}\:{find}\:{the}\:{value}\:{of}\: \\ $$$$\sum_{{k}=\mathrm{1}} ^{{n}} \:\:\:\frac{\mathrm{1}}{{cos}\left({k}\theta\right){cos}\left(\left({k}+\mathrm{1}\right)\theta\right.}\:.\:\:\theta\in{R}. \\ $$

Question Number 28607 Answers: 0 Comments: 0

simplify Σ_(k=0) ^(n−1) 3^k sin^3 ((α/3^(k+1) )) .

$${simplify}\:\:\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\:\mathrm{3}^{{k}} \:{sin}^{\mathrm{3}} \left(\frac{\alpha}{\mathrm{3}^{{k}+\mathrm{1}} }\right)\:. \\ $$$$ \\ $$

Question Number 28611 Answers: 0 Comments: 1

let give θ∈]0,π[ prove that ∫_0 ^1 (dt/(e^(−iθ) −t))= Σ_(n=1) ^(+∞) (e^(inθ) /n) .

$$\left.{let}\:{give}\:\theta\in\right]\mathrm{0},\pi\left[\:\:{prove}\:{that}\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{dt}}{{e}^{−{i}\theta} −{t}}=\:\sum_{{n}=\mathrm{1}} ^{+\infty} \:\:\frac{{e}^{{in}\theta} }{{n}}\:\:.\right. \\ $$

Question Number 28743 Answers: 1 Comments: 2

find the next 4 term and the n^(th) term 1,2,5,26.......

$${find}\:{the}\:{next}\:\mathrm{4}\:{term}\:{and}\:{the} \\ $$$${n}^{{th}} \:{term} \\ $$$$\mathrm{1},\mathrm{2},\mathrm{5},\mathrm{26}....... \\ $$

Question Number 28600 Answers: 0 Comments: 4

Question Number 28597 Answers: 1 Comments: 1

Question Number 28591 Answers: 1 Comments: 0

What is the difference between angular frequency and angular velocity?

$${What}\:{is}\:{the}\:{difference}\:{between} \\ $$$${angular}\:{frequency}\:{and}\:{angular} \\ $$$${velocity}? \\ $$

Question Number 28583 Answers: 1 Comments: 1

Question Number 28574 Answers: 1 Comments: 2

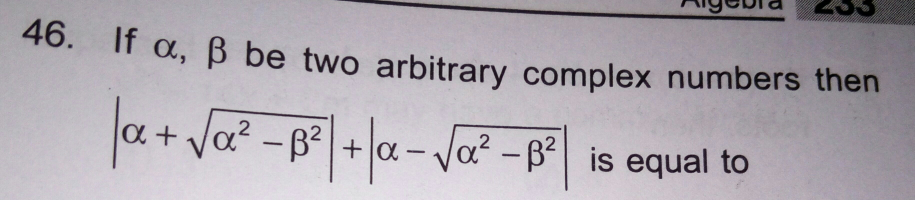
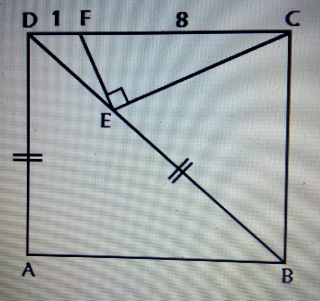
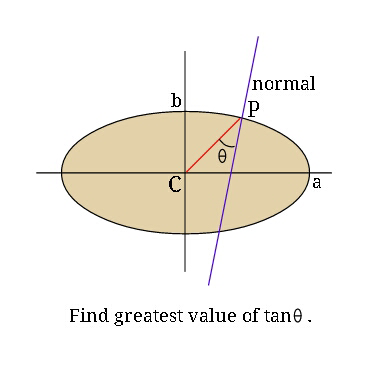
Question Number 28586 Answers: 0 Comments: 0

When dry chlorine is passed thru silver chlorate heated to 90°C then which of the oxide of chlorine is formed and why?

$$\mathrm{When}\:\mathrm{dry}\:\mathrm{chlorine}\:\mathrm{is}\:\mathrm{passed}\:\mathrm{thru} \\ $$$$\mathrm{silver}\:\mathrm{chlorate}\:\mathrm{heated}\:\mathrm{to}\:\mathrm{90}°\mathrm{C} \\ $$$$\mathrm{then}\:\mathrm{which}\:\mathrm{of}\:\mathrm{the}\:\mathrm{oxide}\:\mathrm{of}\:\mathrm{chlorine} \\ $$$$\mathrm{is}\:\mathrm{formed}\:\mathrm{and}\:\mathrm{why}? \\ $$

Question Number 28585 Answers: 1 Comments: 0

Question Number 28565 Answers: 1 Comments: 0

Question Number 28554 Answers: 2 Comments: 0

(((a − b))/((c − d))) = 3 (((a − c))/((b − d))) = 4 (((a − d))/((b − c))) = ?

$$\frac{\left({a}\:−\:{b}\right)}{\left({c}\:−\:{d}\right)}\:\:=\:\:\mathrm{3} \\ $$$$\frac{\left({a}\:−\:{c}\right)}{\left({b}\:−\:{d}\right)}\:\:=\:\:\mathrm{4} \\ $$$$\frac{\left({a}\:−\:{d}\right)}{\left({b}\:−\:{c}\right)}\:\:=\:\:? \\ $$$$ \\ $$

Question Number 28547 Answers: 1 Comments: 0

Question Number 28546 Answers: 0 Comments: 0

let give w=e^(i((2π)/n)) and S= Σ_(k=0) ^(n−1) w^k^2 1) prove that S= Σ_(k=0) ^(n−1) w^((q+k)^2 ) 2) find ∣S∣.

$${let}\:{give}\:{w}={e}^{{i}\frac{\mathrm{2}\pi}{{n}}} \:\:\:{and}\:\:{S}=\:\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\:{w}^{{k}^{\mathrm{2}} } \\ $$$$\left.\mathrm{1}\right)\:{prove}\:{that}\:\:\:{S}=\:\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\:{w}^{\left({q}+{k}\right)^{\mathrm{2}} } \\ $$$$\left.\mathrm{2}\right)\:{find}\:\mid{S}\mid. \\ $$

Question Number 28544 Answers: 0 Comments: 2

if a_1 ,a_2 ,...a_(14 ) are roots of the polynomial p(x)=x^(14) +x^8 2x+1 calculate Σ_(i=1) ^(14) (1/((a_i −1)^2 )) .

$${if}\:\:{a}_{\mathrm{1}} \:,{a}_{\mathrm{2}} ,...{a}_{\mathrm{14}\:} {are}\:{roots}\:{of}\:{the}\:{polynomial} \\ $$$${p}\left({x}\right)={x}^{\mathrm{14}} +{x}^{\mathrm{8}} \:\mathrm{2}{x}+\mathrm{1}\:\:\:{calculate}\:\:\sum_{{i}=\mathrm{1}} ^{\mathrm{14}} \:\:\frac{\mathrm{1}}{\left({a}_{{i}} −\mathrm{1}\right)^{\mathrm{2}} }\:\:. \\ $$

Question Number 28543 Answers: 0 Comments: 0

find the value of ∫_(−∞) ^(+∞) (dt/((t^2 +t +h^2 )^2 +h^2 )) .

$${find}\:{the}\:{value}\:{of}\:\:\int_{−\infty} ^{+\infty} \:\:\:\:\:\:\:\frac{{dt}}{\left({t}^{\mathrm{2}} +{t}\:+{h}^{\mathrm{2}} \right)^{\mathrm{2}} \:+{h}^{\mathrm{2}} }\:\:\:. \\ $$

Question Number 28542 Answers: 0 Comments: 0

if (1/(1−x−y−xy)) = Σ_(n=0) ^∞ g_n (y) x^n find g_n .

$${if}\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{1}−{x}−{y}−{xy}}\:=\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\:{g}_{{n}} \left({y}\right)\:{x}^{{n}} \:\:{find}\:{g}_{{n}} \:\:. \\ $$

Question Number 28541 Answers: 0 Comments: 0

prove that ∫_0 ^∞ ((sinx)/(e^(ax) −1))dx= Σ_(p=1) ^∞ (1/(1+p^2 a^2 )) with a>0

$${prove}\:{that}\:\:\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{sinx}}{{e}^{{ax}} −\mathrm{1}}{dx}=\:\sum_{{p}=\mathrm{1}} ^{\infty} \:\:\frac{\mathrm{1}}{\mathrm{1}+{p}^{\mathrm{2}} {a}^{\mathrm{2}} }\:\:\:\:\:{with}\:{a}>\mathrm{0} \\ $$

Pg 1814 Pg 1815 Pg 1816 Pg 1817 Pg 1818 Pg 1819 Pg 1820 Pg 1821 Pg 1822 Pg 1823

Contact: info@tinkutara.com