
AllQuestion and Answers: Page 1818
Question Number 28597 Answers: 1 Comments: 1

Question Number 28591 Answers: 1 Comments: 0
Question Number 28583 Answers: 1 Comments: 1
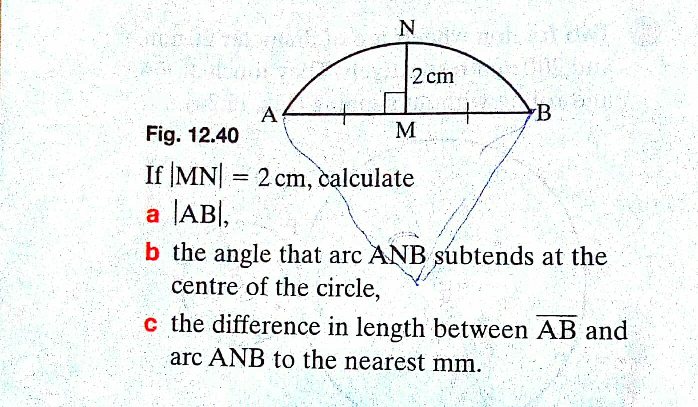
Question Number 28574 Answers: 1 Comments: 2

Question Number 28586 Answers: 0 Comments: 0
Question Number 28585 Answers: 1 Comments: 0

Question Number 28565 Answers: 1 Comments: 0

Question Number 28554 Answers: 2 Comments: 0
Question Number 28547 Answers: 1 Comments: 0

Question Number 28546 Answers: 0 Comments: 0
Question Number 28544 Answers: 0 Comments: 2
Question Number 28543 Answers: 0 Comments: 0
Question Number 28542 Answers: 0 Comments: 0
Question Number 28541 Answers: 0 Comments: 0
Question Number 28539 Answers: 0 Comments: 0
Question Number 28538 Answers: 0 Comments: 0
Question Number 28537 Answers: 0 Comments: 0
Question Number 28536 Answers: 0 Comments: 0
Question Number 28535 Answers: 0 Comments: 0
Question Number 28534 Answers: 0 Comments: 1
Question Number 28533 Answers: 0 Comments: 1
Question Number 28532 Answers: 0 Comments: 1
Question Number 28531 Answers: 0 Comments: 0
Question Number 28530 Answers: 0 Comments: 0
Question Number 28529 Answers: 0 Comments: 2
Question Number 28540 Answers: 0 Comments: 0
Pg 1813 Pg 1814 Pg 1815 Pg 1816 Pg 1817 Pg 1818 Pg 1819 Pg 1820 Pg 1821 Pg 1822
