
AllQuestion and Answers: Page 1814
Question Number 29201 Answers: 2 Comments: 0
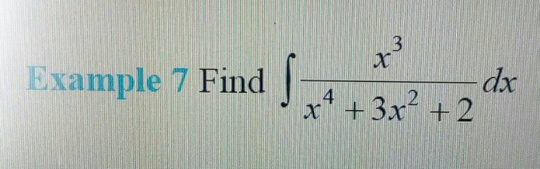
Question Number 29198 Answers: 1 Comments: 1

Question Number 29196 Answers: 0 Comments: 0
Question Number 29231 Answers: 1 Comments: 0

Question Number 29180 Answers: 1 Comments: 0
Question Number 29173 Answers: 1 Comments: 0
Question Number 29172 Answers: 1 Comments: 0
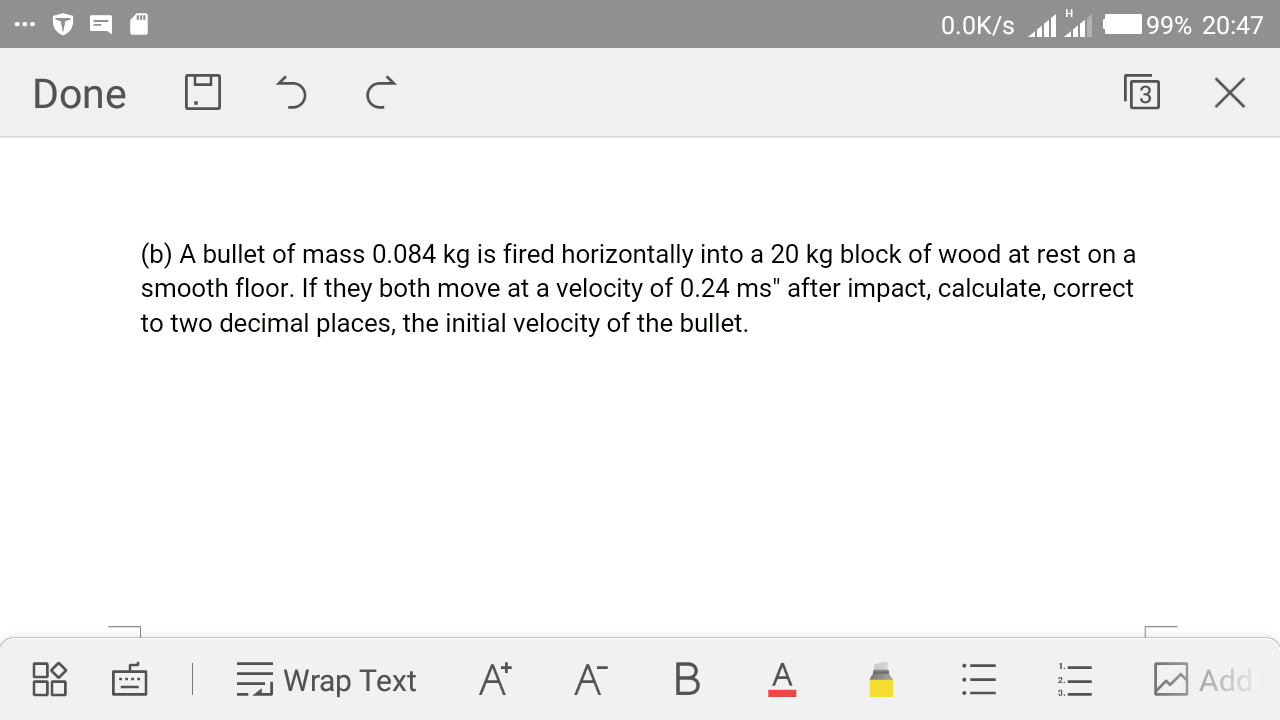
Question Number 29171 Answers: 0 Comments: 0
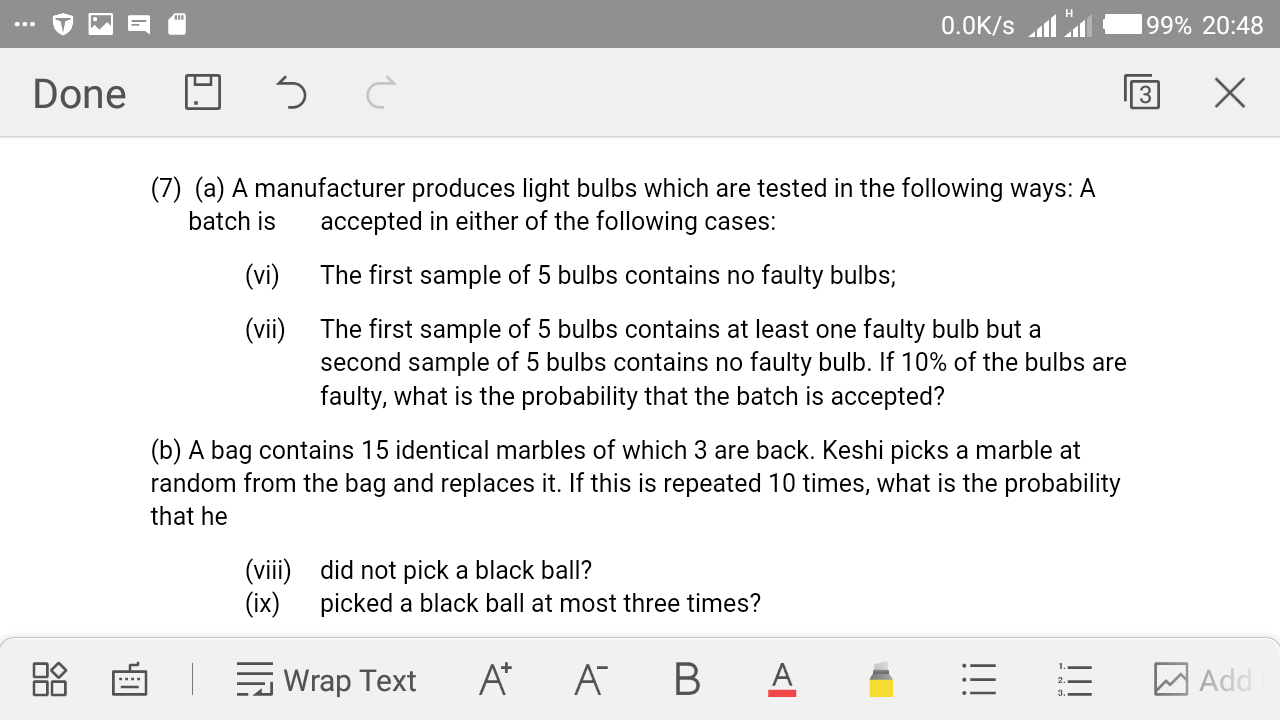
Question Number 29170 Answers: 0 Comments: 0

Question Number 29169 Answers: 0 Comments: 1
Question Number 29168 Answers: 0 Comments: 1

Question Number 29167 Answers: 0 Comments: 1
Question Number 29166 Answers: 0 Comments: 1
Question Number 29165 Answers: 0 Comments: 1
Question Number 29164 Answers: 0 Comments: 1
Question Number 29163 Answers: 0 Comments: 0
Question Number 29162 Answers: 0 Comments: 1
Question Number 29161 Answers: 1 Comments: 1
Question Number 29149 Answers: 1 Comments: 0
Question Number 29148 Answers: 0 Comments: 1
Question Number 29140 Answers: 0 Comments: 6
Question Number 29138 Answers: 0 Comments: 4
Question Number 29134 Answers: 0 Comments: 3

Question Number 29131 Answers: 1 Comments: 2
Question Number 29136 Answers: 0 Comments: 1
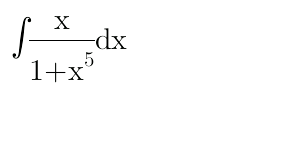
Question Number 29144 Answers: 1 Comments: 0
Pg 1809 Pg 1810 Pg 1811 Pg 1812 Pg 1813 Pg 1814 Pg 1815 Pg 1816 Pg 1817 Pg 1818
