
AllQuestion and Answers: Page 1813
Question Number 28991 Answers: 1 Comments: 1
Question Number 28990 Answers: 0 Comments: 0
Question Number 28989 Answers: 0 Comments: 1
Question Number 28988 Answers: 0 Comments: 0
Question Number 28987 Answers: 0 Comments: 0
Question Number 28986 Answers: 0 Comments: 0
Question Number 28985 Answers: 0 Comments: 0
Question Number 28984 Answers: 0 Comments: 0
Question Number 28983 Answers: 0 Comments: 0
Question Number 28982 Answers: 0 Comments: 0
Question Number 28981 Answers: 1 Comments: 1
Question Number 28980 Answers: 0 Comments: 0
Question Number 29012 Answers: 0 Comments: 1

Question Number 28978 Answers: 0 Comments: 0
Question Number 28977 Answers: 0 Comments: 0
Question Number 28976 Answers: 0 Comments: 0
$${find}\:\int_{−\infty} ^{+\infty} \:\:\:\frac{{cosx}}{{e}^{{x}} +{e}^{−{x}} }{dx}. \\ $$
Question Number 28975 Answers: 0 Comments: 0
Question Number 28960 Answers: 1 Comments: 1

Question Number 28954 Answers: 0 Comments: 0
$${please}\:{solve}\:\mathrm{4},\mathrm{5},\mathrm{6} \\ $$$$ \\ $$
Question Number 28953 Answers: 0 Comments: 0

Question Number 28952 Answers: 0 Comments: 0

Question Number 28949 Answers: 0 Comments: 0
Question Number 28938 Answers: 0 Comments: 3
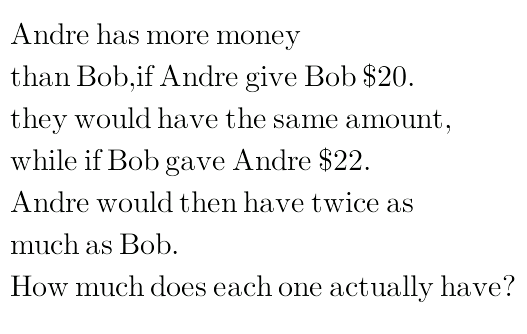
Question Number 28932 Answers: 1 Comments: 0
Question Number 28929 Answers: 1 Comments: 0
Question Number 28930 Answers: 0 Comments: 1

Pg 1808 Pg 1809 Pg 1810 Pg 1811 Pg 1812 Pg 1813 Pg 1814 Pg 1815 Pg 1816 Pg 1817
