
AllQuestion and Answers: Page 1811
Question Number 29445 Answers: 1 Comments: 0
$${find}\:\:\:\int\:\:\:\:\:\:\:\frac{{dx}}{{sinx}\:+{sin}\left(\mathrm{2}{x}\right)}\:. \\ $$
Question Number 29444 Answers: 0 Comments: 1
Question Number 29443 Answers: 1 Comments: 0
Question Number 29442 Answers: 1 Comments: 0
Question Number 29441 Answers: 0 Comments: 1
Question Number 29440 Answers: 0 Comments: 0
Question Number 29439 Answers: 1 Comments: 0
$${find}\:\int_{\mathrm{0}} ^{\pi} \:\frac{{dx}}{\mathrm{2}+{cosx}}\:. \\ $$
Question Number 29433 Answers: 1 Comments: 0
$$\mathrm{4}\left(\mathrm{2x}^{\mathrm{2}} \right)=\mathrm{8}^{\mathrm{x}} \\ $$
Question Number 29420 Answers: 1 Comments: 2

Question Number 29418 Answers: 1 Comments: 1

Question Number 29413 Answers: 1 Comments: 1

Question Number 29415 Answers: 0 Comments: 0

Question Number 29405 Answers: 0 Comments: 1
Question Number 29400 Answers: 2 Comments: 1

Question Number 29384 Answers: 0 Comments: 3
Question Number 29424 Answers: 0 Comments: 8
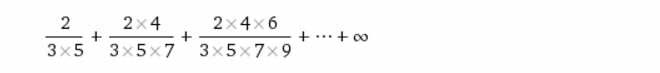
Question Number 29425 Answers: 1 Comments: 1

Question Number 29365 Answers: 1 Comments: 0
Question Number 29364 Answers: 0 Comments: 0
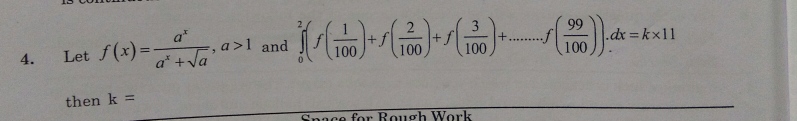
Question Number 29363 Answers: 0 Comments: 1

Question Number 29362 Answers: 1 Comments: 2
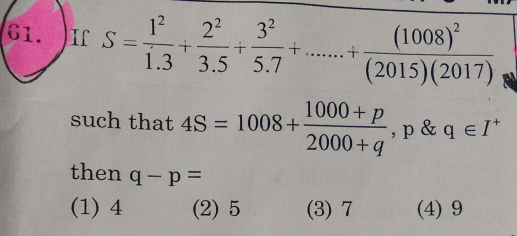
Question Number 29360 Answers: 2 Comments: 1
Question Number 29359 Answers: 1 Comments: 0
Question Number 29354 Answers: 2 Comments: 0
Question Number 29349 Answers: 0 Comments: 1
Question Number 29347 Answers: 0 Comments: 0
Pg 1806 Pg 1807 Pg 1808 Pg 1809 Pg 1810 Pg 1811 Pg 1812 Pg 1813 Pg 1814 Pg 1815
