
AllQuestion and Answers: Page 1810
Question Number 29216 Answers: 1 Comments: 0
Question Number 29213 Answers: 0 Comments: 1
Question Number 29212 Answers: 1 Comments: 1
Question Number 29209 Answers: 1 Comments: 4

Question Number 29202 Answers: 1 Comments: 0
Question Number 29201 Answers: 2 Comments: 0
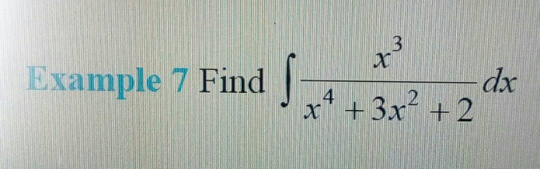
Question Number 29198 Answers: 1 Comments: 1

Question Number 29196 Answers: 0 Comments: 0
Question Number 29231 Answers: 1 Comments: 0

Question Number 29180 Answers: 1 Comments: 0
Question Number 29173 Answers: 1 Comments: 0
Question Number 29172 Answers: 1 Comments: 0
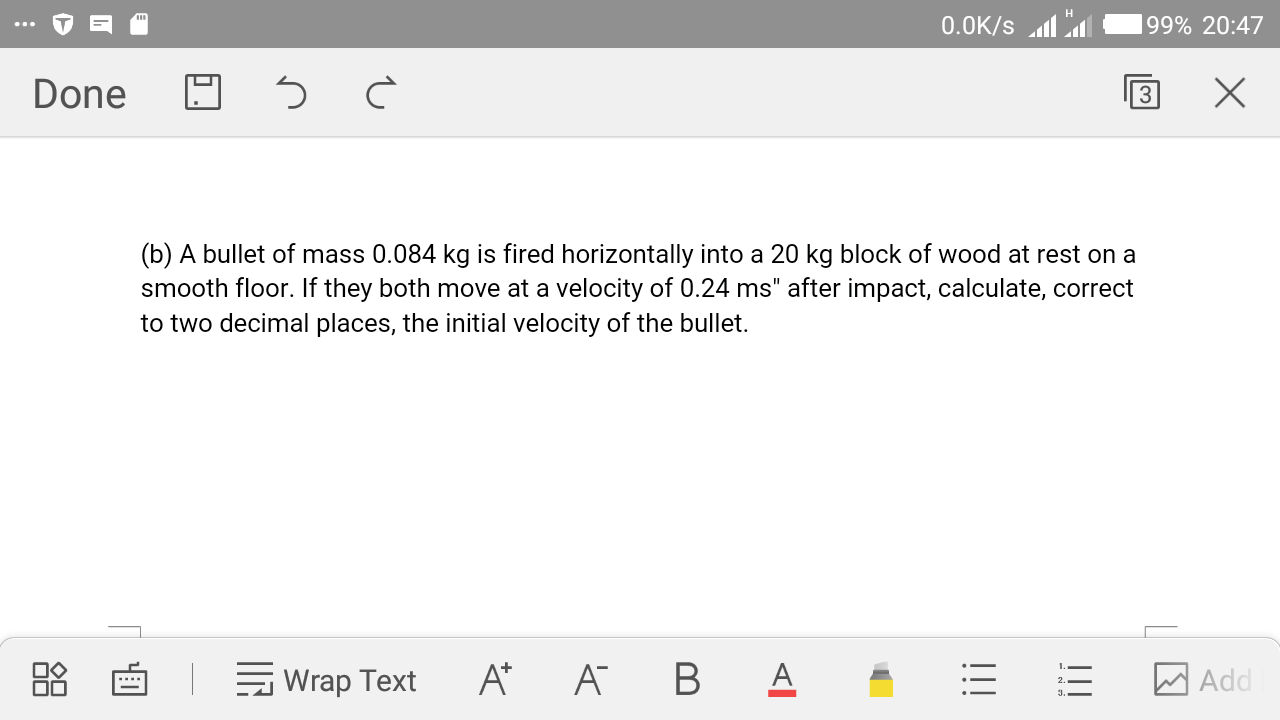
Question Number 29171 Answers: 0 Comments: 0
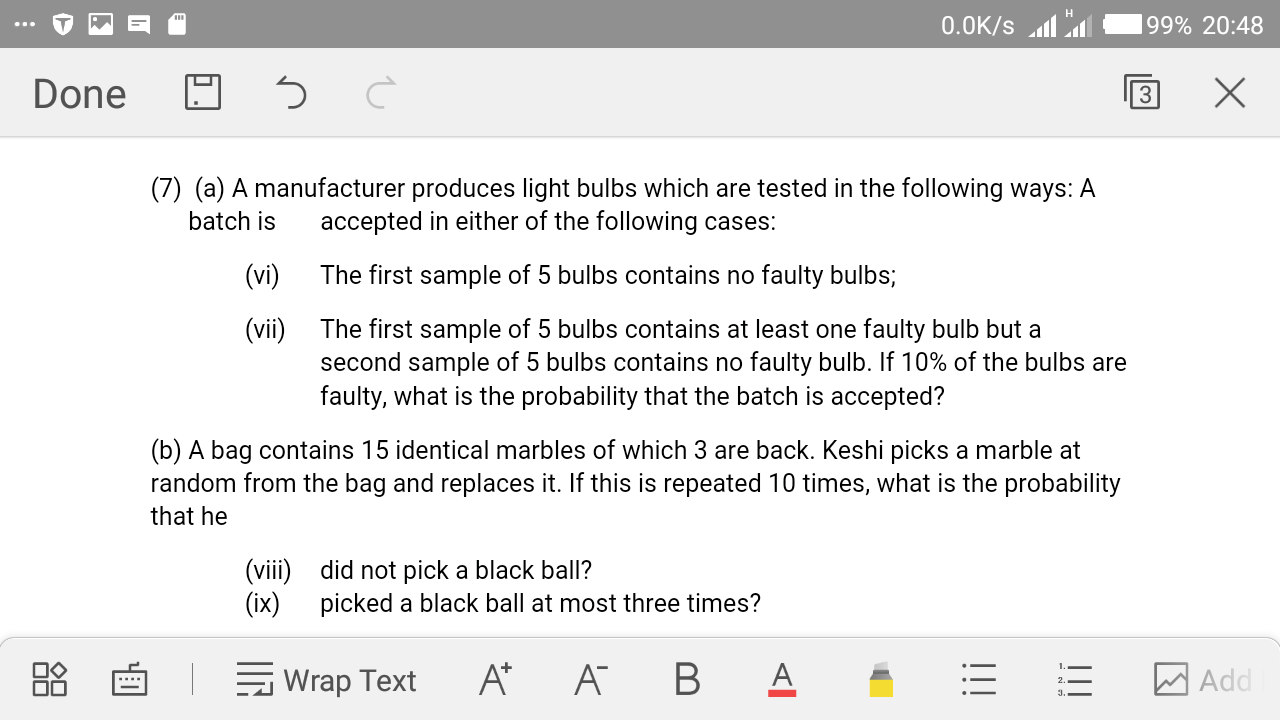
Question Number 29170 Answers: 0 Comments: 0

Question Number 29169 Answers: 0 Comments: 1
Question Number 29168 Answers: 0 Comments: 1

Question Number 29167 Answers: 0 Comments: 1
Question Number 29166 Answers: 0 Comments: 1
Question Number 29165 Answers: 0 Comments: 1
Question Number 29164 Answers: 0 Comments: 1
Question Number 29163 Answers: 0 Comments: 0
Question Number 29162 Answers: 0 Comments: 1
Question Number 29161 Answers: 1 Comments: 1
Question Number 29149 Answers: 1 Comments: 0
Question Number 29148 Answers: 0 Comments: 1
Question Number 29140 Answers: 0 Comments: 6
Pg 1805 Pg 1806 Pg 1807 Pg 1808 Pg 1809 Pg 1810 Pg 1811 Pg 1812 Pg 1813 Pg 1814
