
AllQuestion and Answers: Page 1809
Question Number 29322 Answers: 0 Comments: 5

Question Number 29321 Answers: 0 Comments: 1
Question Number 29320 Answers: 0 Comments: 1
Question Number 29319 Answers: 0 Comments: 0
$$\left.{m}\left.{xmz}\right]\mathrm{33}\right]\mathrm{2}{n}\mathrm{3}{xmxksnd} \\ $$
Question Number 29313 Answers: 0 Comments: 0

Question Number 29311 Answers: 0 Comments: 0
Question Number 29310 Answers: 0 Comments: 0
Question Number 29314 Answers: 0 Comments: 3
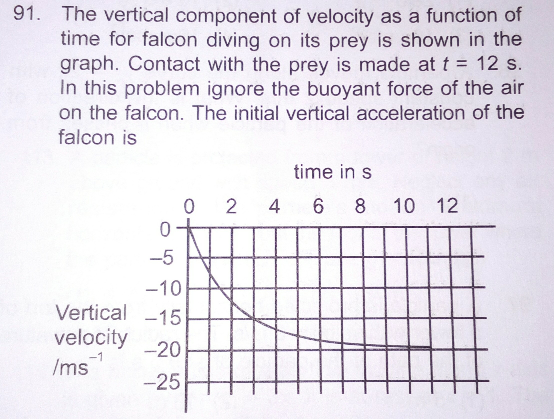
Question Number 29287 Answers: 0 Comments: 0
Question Number 29286 Answers: 0 Comments: 1
Question Number 29276 Answers: 1 Comments: 0
Question Number 29275 Answers: 0 Comments: 0
Question Number 29268 Answers: 0 Comments: 2
Question Number 29272 Answers: 0 Comments: 0
Question Number 29265 Answers: 0 Comments: 0
Question Number 29264 Answers: 1 Comments: 0
Question Number 29273 Answers: 0 Comments: 4

Question Number 29260 Answers: 0 Comments: 0
Question Number 29259 Answers: 1 Comments: 0
Question Number 29308 Answers: 2 Comments: 0
$$\mathrm{Solve}:\:\:\:\mathrm{w}^{\mathrm{3}} \:=\:−\:\mathrm{16} \\ $$
Question Number 29249 Answers: 1 Comments: 1

Question Number 29241 Answers: 1 Comments: 0

Question Number 29242 Answers: 0 Comments: 0

Question Number 29254 Answers: 1 Comments: 1

Question Number 29222 Answers: 1 Comments: 0
$$\mathrm{3}{x}−\mathrm{4}{y}=\mathrm{12},\:{xy}=\mathrm{2} \\ $$
Question Number 29217 Answers: 1 Comments: 0
Pg 1804 Pg 1805 Pg 1806 Pg 1807 Pg 1808 Pg 1809 Pg 1810 Pg 1811 Pg 1812 Pg 1813
