
AllQuestion and Answers: Page 1808
Question Number 29836 Answers: 0 Comments: 0
Question Number 29835 Answers: 0 Comments: 0
Question Number 29834 Answers: 0 Comments: 1
Question Number 29833 Answers: 1 Comments: 0
Question Number 29832 Answers: 0 Comments: 0
Question Number 29821 Answers: 1 Comments: 3
Question Number 29820 Answers: 1 Comments: 3

Question Number 29805 Answers: 0 Comments: 1
Question Number 29818 Answers: 1 Comments: 0
Question Number 29794 Answers: 0 Comments: 9
Question Number 29831 Answers: 0 Comments: 0
Question Number 29786 Answers: 0 Comments: 0

Question Number 29785 Answers: 0 Comments: 0

Question Number 29778 Answers: 1 Comments: 0
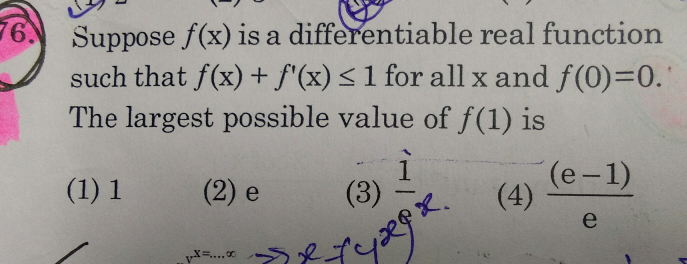
Question Number 29803 Answers: 0 Comments: 3

Question Number 29773 Answers: 0 Comments: 0
$$\underset{\mathrm{x}\rightarrow\mathrm{0},\mathrm{y}\rightarrow\infty} {\mathrm{lim}xy}=? \\ $$
Question Number 29753 Answers: 0 Comments: 0
Question Number 29752 Answers: 0 Comments: 0
Question Number 29770 Answers: 2 Comments: 0
Question Number 29728 Answers: 0 Comments: 8

Question Number 29727 Answers: 1 Comments: 4

Question Number 29776 Answers: 0 Comments: 0

Question Number 29777 Answers: 2 Comments: 5
Question Number 29726 Answers: 0 Comments: 2

Question Number 29887 Answers: 1 Comments: 3
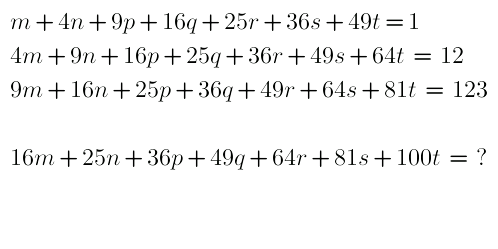
Question Number 29723 Answers: 1 Comments: 1
Pg 1803 Pg 1804 Pg 1805 Pg 1806 Pg 1807 Pg 1808 Pg 1809 Pg 1810 Pg 1811 Pg 1812
