
AllQuestion and Answers: Page 1806
Question Number 30054 Answers: 1 Comments: 0

Question Number 30049 Answers: 0 Comments: 1
Question Number 30045 Answers: 1 Comments: 2

Question Number 30030 Answers: 1 Comments: 2

Question Number 30017 Answers: 1 Comments: 0
Question Number 30008 Answers: 0 Comments: 1
$${integrate}\:{w}.{r}.{t}\:{x} \\ $$$$\int\left({e}^{{x}^{\mathrm{2}} } \right){dx} \\ $$
Question Number 30002 Answers: 0 Comments: 5
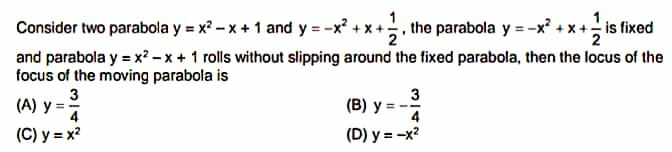
Question Number 29998 Answers: 0 Comments: 0

Question Number 29989 Answers: 1 Comments: 0
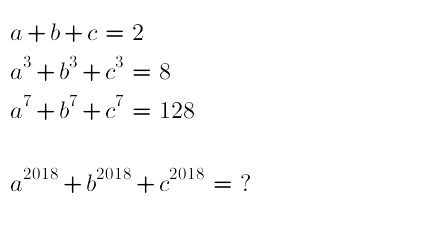
Question Number 29987 Answers: 0 Comments: 0
Question Number 29986 Answers: 1 Comments: 1
$${find}\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\:\frac{{n}+\mathrm{1}}{\mathrm{4}^{{n}} }\:. \\ $$
Question Number 29985 Answers: 0 Comments: 0
Question Number 29984 Answers: 0 Comments: 0
Question Number 29983 Answers: 0 Comments: 1
Question Number 29982 Answers: 0 Comments: 0
Question Number 29981 Answers: 0 Comments: 1
Question Number 29980 Answers: 0 Comments: 0
Question Number 29979 Answers: 0 Comments: 1
Question Number 29978 Answers: 0 Comments: 2
Question Number 29976 Answers: 0 Comments: 0
Question Number 29975 Answers: 0 Comments: 2
Question Number 29974 Answers: 1 Comments: 0
Question Number 29973 Answers: 0 Comments: 1
Question Number 29972 Answers: 0 Comments: 1
Question Number 29971 Answers: 0 Comments: 2
Question Number 29970 Answers: 0 Comments: 1
Pg 1801 Pg 1802 Pg 1803 Pg 1804 Pg 1805 Pg 1806 Pg 1807 Pg 1808 Pg 1809 Pg 1810
