
AllQuestion and Answers: Page 1805
Question Number 29753 Answers: 0 Comments: 0
Question Number 29752 Answers: 0 Comments: 0
Question Number 29770 Answers: 2 Comments: 0
Question Number 29728 Answers: 0 Comments: 8

Question Number 29727 Answers: 1 Comments: 4

Question Number 29776 Answers: 0 Comments: 0

Question Number 29777 Answers: 2 Comments: 5
Question Number 29726 Answers: 0 Comments: 2

Question Number 29887 Answers: 1 Comments: 3
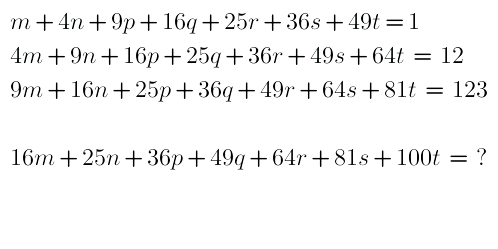
Question Number 29723 Answers: 1 Comments: 1
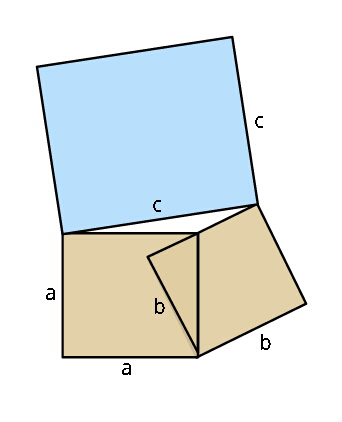
Question Number 29700 Answers: 1 Comments: 0
$$\mathrm{32}^{\mathrm{32}^{\mathrm{32}} } \:/\mathrm{7}...\mathrm{find}\:\mathrm{remainder} \\ $$
Question Number 29689 Answers: 1 Comments: 2
Question Number 29680 Answers: 1 Comments: 0
Question Number 29658 Answers: 1 Comments: 0
Question Number 29648 Answers: 1 Comments: 5
Question Number 29647 Answers: 0 Comments: 1

Question Number 29645 Answers: 1 Comments: 0
Question Number 29646 Answers: 0 Comments: 0
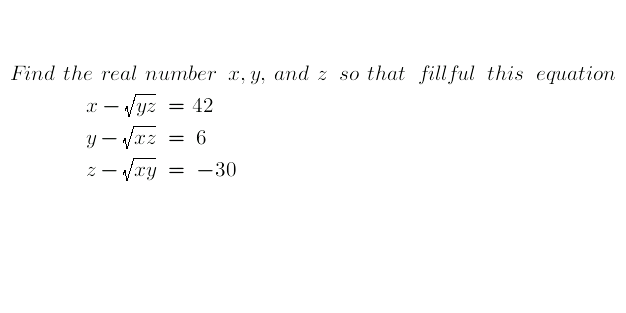
Question Number 29643 Answers: 0 Comments: 0

Question Number 29627 Answers: 1 Comments: 1

Question Number 29633 Answers: 1 Comments: 10
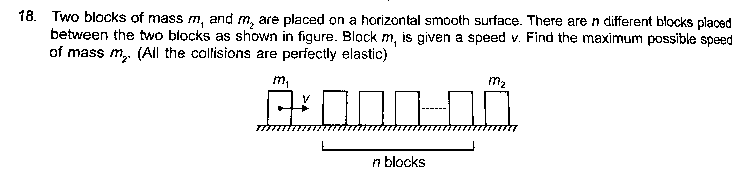
Question Number 29611 Answers: 0 Comments: 4
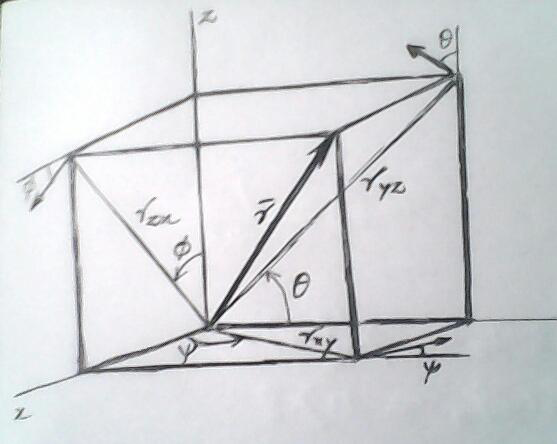
Question Number 29601 Answers: 0 Comments: 0

Question Number 29607 Answers: 0 Comments: 0
Question Number 29581 Answers: 1 Comments: 0
Question Number 29687 Answers: 1 Comments: 4
Pg 1800 Pg 1801 Pg 1802 Pg 1803 Pg 1804 Pg 1805 Pg 1806 Pg 1807 Pg 1808 Pg 1809
