Question and Answers Forum

All Questions Topic List

AllQuestion and Answers: Page 1803

Question Number 30190 Answers: 0 Comments: 0

study the sequence u_(n+1) =(√((1 +u_n ^2 )/2)) with −1<u_0 <1 .

$${study}\:{the}\:{sequence}\:{u}_{{n}+\mathrm{1}} =\sqrt{\frac{\mathrm{1}\:+{u}_{{n}} ^{\mathrm{2}} }{\mathrm{2}}}\:\:\:{with}\:−\mathrm{1}<{u}_{\mathrm{0}} <\mathrm{1}\:. \\ $$

Question Number 30189 Answers: 0 Comments: 0

find lim_(n→∞) n^(−4) Π_(k=1) ^(2n) (n^2 +k^2 )^(1/n) ?.

$${find}\:{lim}_{{n}\rightarrow\infty} \:\:{n}^{−\mathrm{4}} \:\prod_{{k}=\mathrm{1}} ^{\mathrm{2}{n}} \:\left({n}^{\mathrm{2}} \:+{k}^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{{n}}} \:?. \\ $$

Question Number 30188 Answers: 0 Comments: 1

solve x^3 (x^2 +1)y^′ −2xy =0

$$\:{solve}\:{x}^{\mathrm{3}} \left({x}^{\mathrm{2}} \:+\mathrm{1}\right){y}^{'} \:−\mathrm{2}{xy}\:=\mathrm{0} \\ $$

Question Number 30187 Answers: 1 Comments: 0

solve xy^′ −2y = x^4 .

$${solve}\:{xy}^{'} \:−\mathrm{2}{y}\:=\:{x}^{\mathrm{4}} \:. \\ $$

Question Number 30186 Answers: 0 Comments: 0

solve x^2 y^(′′) −2y =x

$${solve}\:{x}^{\mathrm{2}} {y}^{''} \:−\mathrm{2}{y}\:={x} \\ $$

Question Number 30185 Answers: 0 Comments: 0

let I= ∫_0 ^(π/2) ((sinx)/(√(1+sinxcosx)))dx and J= ∫_0 ^(π/2) ((cosx)/(√(1+sinx cosx))) dx 1) calculate I +J 2) find I and J.

$${let}\:\:{I}=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\:\:\frac{{sinx}}{\sqrt{\mathrm{1}+{sinxcosx}}}{dx}\:{and} \\ $$$${J}=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\frac{{cosx}}{\sqrt{\mathrm{1}+{sinx}\:{cosx}}}\:{dx} \\ $$$$\left.\mathrm{1}\right)\:{calculate}\:{I}\:+{J} \\ $$$$\left.\mathrm{2}\right)\:{find}\:{I}\:{and}\:{J}. \\ $$

Question Number 30184 Answers: 0 Comments: 1

find ∫_(1/2) ^2 (1+(1/x^2 ))arctanx dx . (arctan=tan^(−1) ).

$${find}\:\:\int_{\frac{\mathrm{1}}{\mathrm{2}}} ^{\mathrm{2}} \:\left(\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right){arctanx}\:{dx}\:.\:\left({arctan}={tan}^{−\mathrm{1}} \right). \\ $$

Question Number 30183 Answers: 1 Comments: 0

If the roots of the equation ax^2 −bx+5c=0 are in the ratio of 4: 5, then 4b^2 =81ac.

$$\mathrm{If}\:\mathrm{the}\:\mathrm{roots}\:\mathrm{of}\:\mathrm{the}\:\mathrm{equation}\:{ax}^{\mathrm{2}} −{bx}+\mathrm{5}{c}=\mathrm{0} \\ $$$$\mathrm{are}\:\mathrm{in}\:\mathrm{the}\:\mathrm{ratio}\:\mathrm{of}\:\mathrm{4}:\:\mathrm{5},\:\mathrm{then}\:\mathrm{4}{b}^{\mathrm{2}} =\mathrm{81}{ac}. \\ $$

Question Number 30182 Answers: 0 Comments: 2

find ∫_2 ^3 ((√(x+1))/(x(√(1−x))))dx .

$${find}\:\int_{\mathrm{2}} ^{\mathrm{3}} \:\:\:\frac{\sqrt{{x}+\mathrm{1}}}{{x}\sqrt{\mathrm{1}−{x}}}{dx}\:. \\ $$

Question Number 30181 Answers: 0 Comments: 0

find ∫ (dx/(1+x^3 +x^6 )) .

$${find}\:\:\int\:\:\frac{{dx}}{\mathrm{1}+{x}^{\mathrm{3}} \:+{x}^{\mathrm{6}} }\:. \\ $$

Question Number 30180 Answers: 0 Comments: 1

find ∫_0 ^(π/2) ((x sinx cosx)/(tan^2 x +cotan^2 x))dx .(use the ch.x=(π/2) −t).

$${find}\:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\frac{{x}\:{sinx}\:{cosx}}{{tan}^{\mathrm{2}} {x}\:+{cotan}^{\mathrm{2}} {x}}{dx}\:.\left({use}\:{the}\:{ch}.{x}=\frac{\pi}{\mathrm{2}}\:−{t}\right). \\ $$

Question Number 30179 Answers: 0 Comments: 1

find ∫ (dt/(1+cost +sint)) .

$${find}\:\:\int\:\:\:\:\frac{{dt}}{\mathrm{1}+{cost}\:+{sint}}\:\:. \\ $$

Question Number 30178 Answers: 0 Comments: 1

calculate ∫_0 ^(π/2) (dx/(1+cosx cosθ)) with −π<θ<π .

$${calculate}\:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\:\:\frac{{dx}}{\mathrm{1}+{cosx}\:{cos}\theta}\:\:{with}\:−\pi<\theta<\pi\:. \\ $$

Question Number 30177 Answers: 1 Comments: 0

let x∈R and u_n = Π_(k=0) ^n cos((x/2^k )) find a simple form of u_n .

$${let}\:{x}\in{R}\:\:{and}\:{u}_{{n}} =\:\prod_{{k}=\mathrm{0}} ^{{n}} \:{cos}\left(\frac{{x}}{\mathrm{2}^{{k}} }\right)\:{find}\:{a}\:{simple}\:{form}\:{of} \\ $$$${u}_{{n}} . \\ $$

Question Number 30176 Answers: 0 Comments: 0

prove that v_n = Σ_(k=1) ^n (1/(2n+2k +1)) is convergente.

$${prove}\:{that}\:\:{v}_{{n}} =\:\sum_{{k}=\mathrm{1}} ^{{n}} \:\:\:\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{2}{k}\:+\mathrm{1}}\:{is}\:{convergente}. \\ $$

Question Number 30175 Answers: 0 Comments: 2

prove that u_n = Σ_(k=1) ^n (1/(n+k)) is convergente .

$${prove}\:{that}\:{u}_{{n}} =\:\sum_{{k}=\mathrm{1}} ^{{n}} \:\:\frac{\mathrm{1}}{{n}+{k}}\:{is}\:{convergente}\:. \\ $$

Question Number 30174 Answers: 0 Comments: 0

let u_n = Σ_(k=1) ^n (1/k) 1. prove that ln(n+1)≤u_n ≤ln(n) +1 2. show that u_n _(n→∞) ∼ ln(n) .

$${let}\:\:{u}_{{n}} =\:\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{1}}{{k}} \\ $$$$\mathrm{1}.\:{prove}\:{that}\:{ln}\left({n}+\mathrm{1}\right)\leqslant{u}_{{n}} \leqslant{ln}\left({n}\right)\:+\mathrm{1} \\ $$$$\mathrm{2}.\:{show}\:{that}\:{u}_{{n}} \:\:_{{n}\rightarrow\infty} \sim\:{ln}\left({n}\right)\:\:. \\ $$

Question Number 30193 Answers: 0 Comments: 0

let p_n (x)=−1 +Σ_(k=1) ^k x^k 1) prove that the equation p_n (x)=0 have only one solution x_n ∈[0,1] . 2) prove that (x_n ) is decreasing and minored by (1/2) 3) prove that lim_(n→∞) x_n =(1/2) .

$${let}\:{p}_{{n}} \left({x}\right)=−\mathrm{1}\:+\sum_{{k}=\mathrm{1}} ^{{k}} \:{x}^{{k}} \\ $$$$\left.\mathrm{1}\right)\:{prove}\:{that}\:{the}\:{equation}\:{p}_{{n}} \left({x}\right)=\mathrm{0}\:{have}\:{only}\:{one}\: \\ $$$${solution}\:{x}_{{n}} \in\left[\mathrm{0},\mathrm{1}\right]\:. \\ $$$$\left.\mathrm{2}\right)\:{prove}\:{that}\:\left({x}_{{n}} \right)\:{is}\:{decreasing}\:{and}\:{minored}\:{by}\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\left.\mathrm{3}\right)\:{prove}\:{that}\:{lim}_{{n}\rightarrow\infty} \:{x}_{{n}} =\frac{\mathrm{1}}{\mathrm{2}}\:. \\ $$

Question Number 30166 Answers: 0 Comments: 3

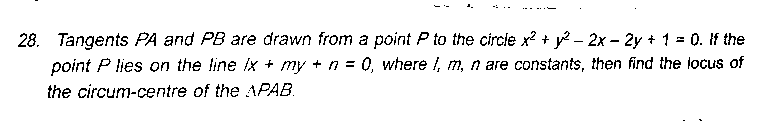
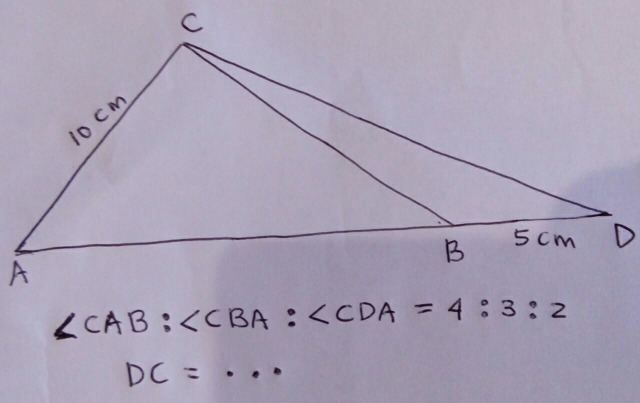
Question Number 30165 Answers: 0 Comments: 3

Question Number 30160 Answers: 0 Comments: 4

Question Number 30159 Answers: 1 Comments: 1

Question Number 30156 Answers: 1 Comments: 0

If x, y, z are in GP and x+3, y+3, z+3 are in HP, then

$$\mathrm{If}\:\:{x},\:{y},\:{z}\:\mathrm{are}\:\mathrm{in}\:\mathrm{GP}\:\mathrm{and}\:{x}+\mathrm{3},\:{y}+\mathrm{3},\:{z}+\mathrm{3}\:\mathrm{are} \\ $$$$\mathrm{in}\:\mathrm{HP},\:\mathrm{then} \\ $$

Question Number 30148 Answers: 2 Comments: 0

how to solve (√((c−(√(−c)))^2 ))+(√((c+6−(√(−c)))^2 )) 2<a<3, −4<b<−3, c=((a+b)/2)

$${how}\:{to}\:{solve}\:\sqrt{\left({c}−\sqrt{−{c}}\right)^{\mathrm{2}} }+\sqrt{\left({c}+\mathrm{6}−\sqrt{−{c}}\right)^{\mathrm{2}} } \\ $$$$\mathrm{2}<{a}<\mathrm{3},\:\:−\mathrm{4}<{b}<−\mathrm{3},\:\:{c}=\frac{{a}+{b}}{\mathrm{2}} \\ $$

Question Number 30129 Answers: 0 Comments: 1

Question Number 30123 Answers: 0 Comments: 3

find the convergence or divergence Σ_(n = 1) ^∞ (((n − 1)/n))

$$\mathrm{find}\:\mathrm{the}\:\mathrm{convergence}\:\mathrm{or}\:\mathrm{divergence}\:\:\:\:\:\underset{\mathrm{n}\:=\:\mathrm{1}} {\overset{\infty} {\sum}}\:\left(\frac{\mathrm{n}\:−\:\mathrm{1}}{\mathrm{n}}\right) \\ $$

Pg 1798 Pg 1799 Pg 1800 Pg 1801 Pg 1802 Pg 1803 Pg 1804 Pg 1805 Pg 1806 Pg 1807

Terms of Service

Contact: info@tinkutara.com