Question and Answers Forum

AllQuestion and Answers: Page 1802

Question Number 28888 Answers: 0 Comments: 0

find I_n = ∫_0 ^π (dx/(1+cos^2 (nx))) with n∈ N^★ .

$${find}\:\:{I}_{{n}} =\:\int_{\mathrm{0}} ^{\pi} \:\:\:\frac{{dx}}{\mathrm{1}+{cos}^{\mathrm{2}} \left({nx}\right)}\:{with}\:{n}\in\:{N}^{\bigstar} . \\ $$

Question Number 28887 Answers: 0 Comments: 2

find ∫ arcsin((√(x/(x+2))))dx.

$${find}\:\int\:\:{arcsin}\left(\sqrt{\frac{{x}}{{x}+\mathrm{2}}}\right){dx}. \\ $$

Question Number 28886 Answers: 1 Comments: 0

find ∫ (x/(cos^2 x))dx.

$${find}\:\int\:\:\:\frac{{x}}{{cos}^{\mathrm{2}} {x}}{dx}. \\ $$

Question Number 28885 Answers: 0 Comments: 1

find ∫_(−1) ^1 (dt/(t +(√(1+t^2 )))) .

$${find}\:\:\int_{−\mathrm{1}} ^{\mathrm{1}} \:\:\:\:\frac{{dt}}{{t}\:+\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }}\:. \\ $$

Question Number 28884 Answers: 0 Comments: 0

find ∫_0 ^(π/2) cost ln(tant)dt.

$${find}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:{cost}\:{ln}\left({tant}\right){dt}. \\ $$

Question Number 28883 Answers: 0 Comments: 1

find ∫_0 ^∞ (dt/((1+t^2 )^4 ))

$${find}\:\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{dt}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{4}} } \\ $$

Question Number 28882 Answers: 0 Comments: 2

find ∫_(−π) ^π ((2dt)/(2+sint +cost)) .

$${find}\:\int_{−\pi} ^{\pi} \:\:\:\frac{\mathrm{2}{dt}}{\mathrm{2}+{sint}\:+{cost}}\:. \\ $$

Question Number 28881 Answers: 1 Comments: 0

find ∫_(−∞) ^(+∞) (dt/(t^2 +2t+2))

$${find}\:\int_{−\infty} ^{+\infty} \:\:\:\:\frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{2}{t}+\mathrm{2}} \\ $$

Question Number 28879 Answers: 0 Comments: 0

find the value of Σ_(n=1) ^(+∞) ((cos(nπx))/n^2 ) with 0<x<1.

$${find}\:{the}\:{value}\:{of}\:\sum_{{n}=\mathrm{1}} ^{+\infty} \:\:\frac{{cos}\left({n}\pi{x}\right)}{{n}^{\mathrm{2}} }\:{with}\:\:\mathrm{0}<{x}<\mathrm{1}. \\ $$

Question Number 28876 Answers: 0 Comments: 1

Evaluate (i) lim_(x→−∞) ((2−3x)/(√(3+4x^2 ))) (ii) lim_(x→+∞) ((2−3x)/(√(3+4x^2 )))

$$\mathcal{E}{valuate} \\ $$$$\left(\mathrm{i}\right)\:\:\underset{{x}\rightarrow−\infty} {{lim}}\:\:\frac{\mathrm{2}−\mathrm{3x}}{\sqrt{\mathrm{3}+\mathrm{4x}^{\mathrm{2}} }} \\ $$$$\left(\mathrm{ii}\right)\:\:\underset{{x}\rightarrow+\infty} {{lim}}\:\:\frac{\mathrm{2}−\mathrm{3x}}{\sqrt{\mathrm{3}+\mathrm{4x}^{\mathrm{2}} }} \\ $$

Question Number 28858 Answers: 0 Comments: 1

Question Number 28857 Answers: 1 Comments: 0

Question Number 28856 Answers: 0 Comments: 0

Question Number 28854 Answers: 0 Comments: 0

The arms of an ac maxwell bridge are arranged as follows: AB is a non - active resistance of 1000 Ω in parallel with a capacitor of capacitance of 0.5μF , BC is a non - inductive resistance of 600 Ω, CD is inductive impedance (unknown) and DA is a non - inductive resustance of 400 Ω. If balance is obtained under these conditions. Find the value of the resistance and the inductance of the branch CD and show the circuit diagram.

$$\mathrm{The}\:\mathrm{arms}\:\mathrm{of}\:\mathrm{an}\:\mathrm{ac}\:\mathrm{maxwell}\:\mathrm{bridge}\:\mathrm{are}\:\mathrm{arranged}\:\mathrm{as}\:\mathrm{follows}:\:\:\mathrm{AB}\:\:\mathrm{is}\:\mathrm{a}\:\mathrm{non}\:-\:\mathrm{active} \\ $$$$\mathrm{resistance}\:\mathrm{of}\:\:\:\mathrm{1000}\:\Omega\:\:\mathrm{in}\:\mathrm{parallel}\:\mathrm{with}\:\mathrm{a}\:\mathrm{capacitor}\:\mathrm{of}\:\mathrm{capacitance}\:\mathrm{of}\:\:\:\mathrm{0}.\mathrm{5}\mu\mathrm{F}\:, \\ $$$$\mathrm{BC}\:\:\mathrm{is}\:\mathrm{a}\:\mathrm{non}\:-\:\mathrm{inductive}\:\mathrm{resistance}\:\mathrm{of}\:\:\mathrm{600}\:\Omega,\:\:\:\mathrm{CD}\:\mathrm{is}\:\mathrm{inductive}\:\mathrm{impedance}\:\left(\mathrm{unknown}\right) \\ $$$$\mathrm{and}\:\mathrm{DA}\:\:\mathrm{is}\:\mathrm{a}\:\mathrm{non}\:-\:\mathrm{inductive}\:\mathrm{resustance}\:\mathrm{of}\:\:\mathrm{400}\:\Omega.\:\:\mathrm{If}\:\mathrm{balance}\:\mathrm{is}\:\mathrm{obtained}\:\mathrm{under} \\ $$$$\mathrm{these}\:\mathrm{conditions}.\:\mathrm{Find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\mathrm{the}\:\mathrm{resistance}\:\mathrm{and}\:\mathrm{the}\:\mathrm{inductance}\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{branch}\:\:\mathrm{CD}\:\:\mathrm{and}\:\mathrm{show}\:\mathrm{the}\:\mathrm{circuit}\:\mathrm{diagram}. \\ $$

Question Number 28852 Answers: 0 Comments: 0

Testing of a Bakelite sample by schering Bridge having a standard capacitor of 106pF , balance was obtained with a capacitance of 0.351 F in parallel with non - inductive resistance in the remaining arm of the bridge being 130 Ω. Determine the capacitance and the equivalent series resistance of the specimen and draw the circuit diagram.

$$\mathrm{Testing}\:\mathrm{of}\:\mathrm{a}\:\mathrm{Bakelite}\:\mathrm{sample}\:\mathrm{by}\:\mathrm{schering}\:\mathrm{Bridge}\:\mathrm{having}\:\mathrm{a}\:\mathrm{standard}\:\mathrm{capacitor} \\ $$$$\mathrm{of}\:\:\mathrm{106pF}\:,\:\:\mathrm{balance}\:\mathrm{was}\:\mathrm{obtained}\:\mathrm{with}\:\mathrm{a}\:\mathrm{capacitance}\:\mathrm{of}\:\:\:\mathrm{0}.\mathrm{351}\:\mathrm{F}\:\:\mathrm{in}\:\mathrm{parallel} \\ $$$$\mathrm{with}\:\mathrm{non}\:-\:\mathrm{inductive}\:\mathrm{resistance}\:\mathrm{in}\:\mathrm{the}\:\mathrm{remaining}\:\mathrm{arm}\:\mathrm{of}\:\mathrm{the}\:\mathrm{bridge}\:\mathrm{being}\:\:\:\mathrm{130}\:\Omega. \\ $$$$\mathrm{Determine}\:\mathrm{the}\:\mathrm{capacitance}\:\mathrm{and}\:\mathrm{the}\:\mathrm{equivalent}\:\mathrm{series}\:\mathrm{resistance}\:\mathrm{of}\:\mathrm{the}\:\mathrm{specimen} \\ $$$$\mathrm{and}\:\mathrm{draw}\:\mathrm{the}\:\mathrm{circuit}\:\mathrm{diagram}. \\ $$

Question Number 28833 Answers: 0 Comments: 0

let give ϕ(x) =x ,ϕ 2π periodique even developp f at fourier series then find the value of Σ_(n=1) ^∞ (((−1)^n )/n^2 ) and Σ_(n=0) ^∞ (1/((2n+1)^2 )) .

$${let}\:{give}\:\varphi\left({x}\right)\:={x}\:,\varphi\:\mathrm{2}\pi\:{periodique}\:{even} \\ $$$${developp}\:{f}\:{at}\:{fourier}\:{series}\:{then}\:{find}\:{the}\:{value}\:{of} \\ $$$$\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}^{\mathrm{2}} }\:{and}\:\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }\:. \\ $$

Question Number 28832 Answers: 0 Comments: 0

find the value of A_n = ∫_1 ^(+∞) (dt/(t^(n+1) (√(t−1)))) .withn∈N .

$${find}\:{the}\:{value}\:{of}\:\:{A}_{{n}} =\:\int_{\mathrm{1}} ^{+\infty} \:\:\:\frac{{dt}}{{t}^{{n}+\mathrm{1}} \sqrt{{t}−\mathrm{1}}}\:.{withn}\in{N}\:. \\ $$

Question Number 28835 Answers: 1 Comments: 4

Question Number 28830 Answers: 0 Comments: 0

let give f(x)= ch(αx) and 2π periodic with α≠0 developp f at fourier series.

$${let}\:{give}\:{f}\left({x}\right)=\:{ch}\left(\alpha{x}\right)\:{and}\:\mathrm{2}\pi\:{periodic}\:{with}\:\alpha\neq\mathrm{0} \\ $$$${developp}\:{f}\:{at}\:{fourier}\:{series}. \\ $$

Question Number 28828 Answers: 0 Comments: 0

find f(x)=∫_0 ^1 ln(1+xt^2 )dt with ∣x∣<1 .

$${find}\:{f}\left({x}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:{ln}\left(\mathrm{1}+{xt}^{\mathrm{2}} \right){dt}\:{with}\:\mid{x}\mid<\mathrm{1}\:. \\ $$

Question Number 28827 Answers: 0 Comments: 0

let give F(x)=∫_0 ^∞ ((arctan(1+x(1+t^2 )))/(1+t^2 ))dt and x>0 calculate (dF/dx)(x).

$${let}\:{give}\:{F}\left({x}\right)=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{arctan}\left(\mathrm{1}+{x}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\right)}{\mathrm{1}+{t}^{\mathrm{2}} }{dt}\:\:{and}\:{x}>\mathrm{0} \\ $$$${calculate}\:\frac{{dF}}{{dx}}\left({x}\right).\:\: \\ $$

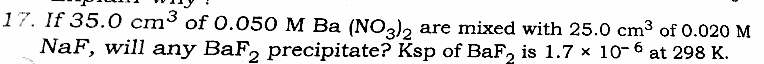
Question Number 28826 Answers: 0 Comments: 0

let give f(x)= e^(−x) cosx and 2π periodic 1) developp f at fourier series 2) find the value of Σ_(n=−∞) ^(n=+∞) (((−1)^n )/(1+n^2 )) .

$${let}\:{give}\:{f}\left({x}\right)=\:{e}^{−{x}} \:{cosx}\:\:{and}\:\mathrm{2}\pi\:{periodic} \\ $$$$\left.\mathrm{1}\right)\:{developp}\:{f}\:{at}\:{fourier}\:{series} \\ $$$$\left.\mathrm{2}\right)\:{find}\:{the}\:{value}\:{of}\:\:\sum_{{n}=−\infty} ^{{n}=+\infty} \:\:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{1}+{n}^{\mathrm{2}} }\:. \\ $$

Question Number 28825 Answers: 0 Comments: 0

let give f(x)= e^(−x) cosx prove that f(x)= Σ_(n=0) ^∞ ((((√2))^n )/(n!)) cos(((3nπ)/4)) x^n .

$${let}\:{give}\:{f}\left({x}\right)=\:{e}^{−{x}} \:{cosx}\:{prove}\:{that} \\ $$$${f}\left({x}\right)=\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\:\:\frac{\left(\sqrt{\mathrm{2}}\right)^{{n}} }{{n}!}\:{cos}\left(\frac{\mathrm{3}{n}\pi}{\mathrm{4}}\right)\:{x}^{{n}} \:\:. \\ $$

Question Number 28824 Answers: 0 Comments: 0

by using residus theorem find the value of A_n = ∫_0 ^∞ (dx/(1+x^n )) with n integr and n≥2.

$${by}\:{using}\:{residus}\:{theorem}\:{find}\:{the}\:{value}\:{of} \\ $$$${A}_{{n}} =\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dx}}{\mathrm{1}+{x}^{{n}} }\:\:{with}\:{n}\:{integr}\:{and}\:{n}\geqslant\mathrm{2}. \\ $$

Question Number 28823 Answers: 0 Comments: 0

find I = ∫_(−∞) ^(+∞) (((x−1)cosx)/(x^2 −2x+2))dx and J= ∫_(−∞) ^(+∞) (((x−1)sinx)/(x^2 −2x +2)) dx.

$${find}\:\:{I}\:=\:\int_{−\infty} ^{+\infty} \:\:\frac{\left({x}−\mathrm{1}\right){cosx}}{{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{2}}{dx}\:{and} \\ $$$${J}=\:\int_{−\infty} ^{+\infty} \:\:\frac{\left({x}−\mathrm{1}\right){sinx}}{{x}^{\mathrm{2}} −\mathrm{2}{x}\:+\mathrm{2}}\:{dx}. \\ $$

Question Number 28821 Answers: 0 Comments: 0

find the value of ∫_0 ^(2π) ((4 cos(4θ))/(5−4cosθ)) dθ .

$${find}\:{the}\:{value}\:{of}\:\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\frac{\mathrm{4}\:{cos}\left(\mathrm{4}\theta\right)}{\mathrm{5}−\mathrm{4}{cos}\theta}\:{d}\theta\:. \\ $$

Pg 1797 Pg 1798 Pg 1799 Pg 1800 Pg 1801 Pg 1802 Pg 1803 Pg 1804 Pg 1805 Pg 1806

Contact: info@tinkutara.com