
AllQuestion and Answers: Page 1801
Question Number 30193 Answers: 0 Comments: 0
Question Number 30166 Answers: 0 Comments: 3
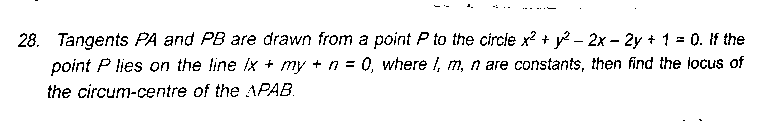
Question Number 30165 Answers: 0 Comments: 3

Question Number 30160 Answers: 0 Comments: 4

Question Number 30159 Answers: 1 Comments: 1
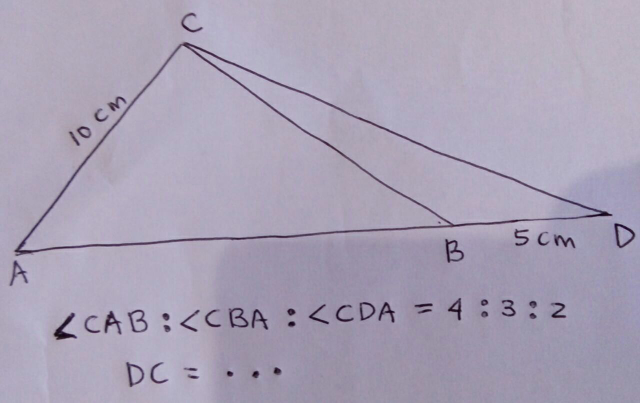
Question Number 30156 Answers: 1 Comments: 0
Question Number 30148 Answers: 2 Comments: 0
Question Number 30129 Answers: 0 Comments: 1

Question Number 30123 Answers: 0 Comments: 3
Question Number 30120 Answers: 2 Comments: 1

Question Number 30119 Answers: 2 Comments: 1
Question Number 30106 Answers: 1 Comments: 0
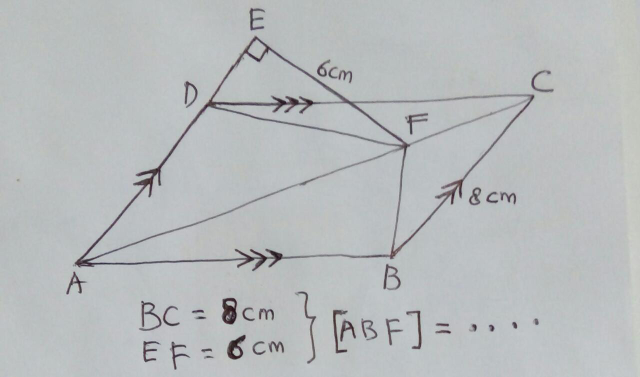
Question Number 30094 Answers: 0 Comments: 5
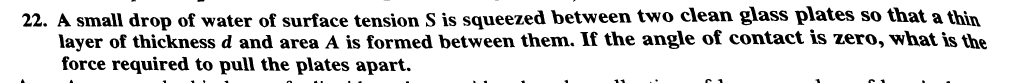
Question Number 30092 Answers: 1 Comments: 0
Question Number 30173 Answers: 0 Comments: 1
Question Number 30090 Answers: 1 Comments: 0
Question Number 30089 Answers: 0 Comments: 0
Question Number 30087 Answers: 3 Comments: 0
Question Number 30079 Answers: 4 Comments: 1

Question Number 30054 Answers: 1 Comments: 0

Question Number 30049 Answers: 0 Comments: 1
Question Number 30045 Answers: 1 Comments: 2

Question Number 30030 Answers: 1 Comments: 2

Question Number 30017 Answers: 1 Comments: 0
Question Number 30008 Answers: 0 Comments: 1
$${integrate}\:{w}.{r}.{t}\:{x} \\ $$$$\int\left({e}^{{x}^{\mathrm{2}} } \right){dx} \\ $$
Question Number 30002 Answers: 0 Comments: 5
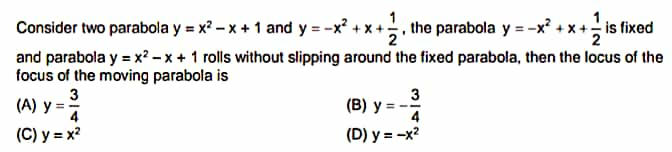
Pg 1796 Pg 1797 Pg 1798 Pg 1799 Pg 1800 Pg 1801 Pg 1802 Pg 1803 Pg 1804 Pg 1805
