
AllQuestion and Answers: Page 1799
Question Number 30550 Answers: 0 Comments: 0
Question Number 30549 Answers: 0 Comments: 0
Question Number 30548 Answers: 0 Comments: 0
Question Number 30547 Answers: 0 Comments: 0
Question Number 30546 Answers: 0 Comments: 0
Question Number 30545 Answers: 0 Comments: 0
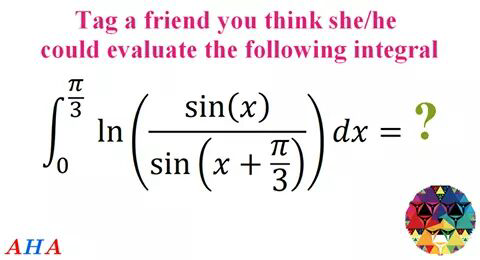
Question Number 30544 Answers: 0 Comments: 0
$${find}\:{I}=\:\int_{\mathrm{0}} ^{\pi} \:\:\frac{{t}}{\mathrm{2}+{sint}}{dt}. \\ $$
Question Number 30543 Answers: 1 Comments: 1
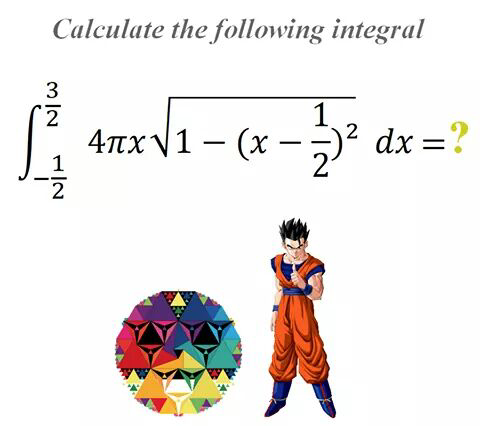
Question Number 30542 Answers: 0 Comments: 0
Question Number 30541 Answers: 0 Comments: 0
Question Number 30540 Answers: 0 Comments: 0
Question Number 30538 Answers: 1 Comments: 0
Question Number 30626 Answers: 0 Comments: 6

Question Number 30529 Answers: 0 Comments: 0
Question Number 30528 Answers: 1 Comments: 1
$${simplify}\:\:{A}=\:{arctan}\left(\frac{{sinx}}{\mathrm{1}−{cosx}}\right)\:. \\ $$
Question Number 30527 Answers: 1 Comments: 0
Question Number 30526 Answers: 0 Comments: 0
Question Number 30525 Answers: 0 Comments: 0
Question Number 30524 Answers: 1 Comments: 2
Question Number 30523 Answers: 0 Comments: 0
Question Number 30522 Answers: 1 Comments: 1
Question Number 30521 Answers: 0 Comments: 2
Question Number 30519 Answers: 1 Comments: 0
Question Number 30518 Answers: 1 Comments: 0
Question Number 30517 Answers: 0 Comments: 1
Question Number 30515 Answers: 0 Comments: 0
Pg 1794 Pg 1795 Pg 1796 Pg 1797 Pg 1798 Pg 1799 Pg 1800 Pg 1801 Pg 1802 Pg 1803
