
AllQuestion and Answers: Page 1798
Question Number 30438 Answers: 0 Comments: 0
Question Number 30435 Answers: 0 Comments: 0
Question Number 30434 Answers: 0 Comments: 0
$${find}\:{the}\:{nature}\:{of}\:\:\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\:{x}^{{n}!} \:. \\ $$
Question Number 30433 Answers: 0 Comments: 0
Question Number 30432 Answers: 0 Comments: 0
Question Number 30431 Answers: 0 Comments: 0
Question Number 30429 Answers: 0 Comments: 1
$${What}\:{are}\:{the}\:{conditions}\:{for}\:{using} \\ $$$${L}'{hospital}\:{rule}? \\ $$
Question Number 30428 Answers: 0 Comments: 0
Question Number 30427 Answers: 0 Comments: 6
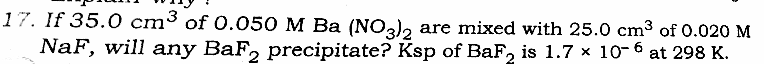
Question Number 30426 Answers: 0 Comments: 0
Question Number 30424 Answers: 0 Comments: 0
Question Number 30423 Answers: 0 Comments: 0
Question Number 30422 Answers: 0 Comments: 0
$${integrate}\:{the}\:{d}.{e}.\:{y}^{'} \:\mathrm{2}{ty}=\:{sint} \\ $$
Question Number 30421 Answers: 1 Comments: 0
$${integrate}\:{y}^{'} −\mathrm{2}{ty}\:+{ty}^{\mathrm{2}} =\mathrm{0} \\ $$
Question Number 30420 Answers: 1 Comments: 0
Question Number 30419 Answers: 1 Comments: 0
Question Number 30418 Answers: 0 Comments: 0
Question Number 30417 Answers: 0 Comments: 0
Question Number 30416 Answers: 0 Comments: 0
$${integrate}\:{the}\:{d}.{e}.\:\:\:{y}^{''} \:−\mathrm{4}{y}\:={x}\:+{e}^{\mathrm{2}{x}} . \\ $$
Question Number 30415 Answers: 0 Comments: 0
Question Number 30414 Answers: 0 Comments: 0
Question Number 30413 Answers: 0 Comments: 0
Question Number 30412 Answers: 0 Comments: 0
Question Number 30411 Answers: 0 Comments: 0
$${solve}\:{the}\:{d}.{e}.\:{y}+{x}\:\left({y}^{'} \right)^{\mathrm{3}} =\mathrm{0} \\ $$
Question Number 30409 Answers: 0 Comments: 0
Question Number 30408 Answers: 0 Comments: 0
$${integrate}\:{the}\:{d}.{e}.\:{y}^{'} {sinx}\:−\mathrm{2}{y}\:{cosx}={e}^{−{x}} . \\ $$
Pg 1793 Pg 1794 Pg 1795 Pg 1796 Pg 1797 Pg 1798 Pg 1799 Pg 1800 Pg 1801 Pg 1802
