Question and Answers Forum

All Questions Topic List

AllQuestion and Answers: Page 1794

Question Number 29415 Answers: 0 Comments: 0

Question Number 29405 Answers: 0 Comments: 1

Fluids

$${Fluids} \\ $$

Question Number 29400 Answers: 2 Comments: 1

Question Number 29384 Answers: 0 Comments: 3

Please can it be proven by another means that ∫tan^2 xdx=tanx+x +c

$${Please}\:{can}\:{it}\:{be}\:{proven}\:{by}\:{another} \\ $$$${means}\:{that}\: \\ $$$$ \\ $$$$\:\:\:\:\:\int\mathrm{tan}\:^{\mathrm{2}} {xdx}={tanx}+{x}\:+{c} \\ $$

Question Number 29424 Answers: 0 Comments: 8

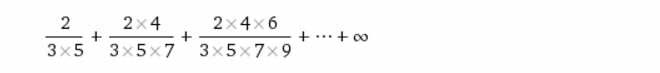
Question Number 29425 Answers: 1 Comments: 1

Question Number 29365 Answers: 1 Comments: 0

the line x+y=2 cuts a circle x^2 +y^(2 ) =4 at two points. find the co−ordinates of points.

$${the}\:{line}\:{x}+{y}=\mathrm{2}\:{cuts}\:{a}\:{circle}\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}\:} =\mathrm{4}\:{at}\:{two}\:{points}.\:{find}\:{the}\:{co}−{ordinates}\:{of}\:{points}. \\ $$

Question Number 29364 Answers: 0 Comments: 0

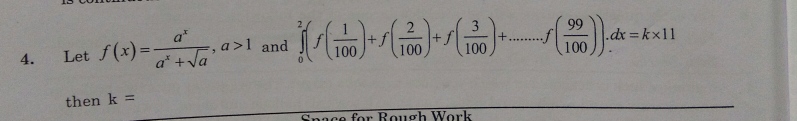
Question Number 29363 Answers: 0 Comments: 1

Question Number 29362 Answers: 1 Comments: 2

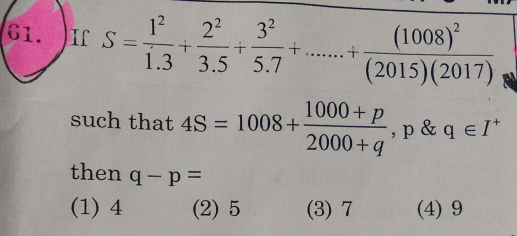
Question Number 29360 Answers: 2 Comments: 1

Two stones are thrown up simultaneously from the edge of a cliff 200m high with initial speeds of 15ms^(−1) and 30ms^(−1) . Verify that the graph shown below correctly represents the time variation of the relative position of the second stone with respect to the first.Neglect air resistance and assume that the stones do not rebound.Take g=10m/s^2 . Give the equations of the linear and curved parts of the plot.

$${Two}\:{stones}\:{are}\:{thrown}\:{up}\: \\ $$$${simultaneously}\:{from}\:{the}\:{edge}\:{of} \\ $$$${a}\:{cliff}\:\mathrm{200}{m}\:{high}\:{with}\:{initial} \\ $$$${speeds}\:{of}\:\mathrm{15}{ms}^{−\mathrm{1}} \:{and}\:\mathrm{30}{ms}^{−\mathrm{1}} . \\ $$$${Verify}\:{that}\:{the}\:{graph}\:{shown} \\ $$$${below}\:{correctly}\:{represents}\:{the} \\ $$$${time}\:{variation}\:{of}\:{the}\:{relative} \\ $$$${position}\:{of}\:{the}\:{second}\:{stone} \\ $$$${with}\:{respect}\:{to}\:{the}\:{first}.{Neglect} \\ $$$${air}\:{resistance}\:{and}\:{assume}\:{that} \\ $$$${the}\:{stones}\:{do}\:{not}\:{rebound}.{Take} \\ $$$${g}=\mathrm{10}{m}/{s}^{\mathrm{2}} .\:{Give}\:{the}\:{equations}\:{of} \\ $$$${the}\:{linear}\:{and}\:{curved}\:{parts}\:{of} \\ $$$${the}\:{plot}. \\ $$

Question Number 29359 Answers: 1 Comments: 0

On a two lane road,car A is travelling with a speed of 36km/h. Two cars B and C approach A in opposite directions with a speed of 54km/h each.At a certain instant, when the distance AB is equal to AC,both being 1km,B decides to overtake A before C does.What minimum acceleration of carB is required to avoid an accident?

$${On}\:{a}\:{two}\:{lane}\:{road},{car}\:{A}\:{is} \\ $$$${travelling}\:{with}\:{a}\:{speed}\:{of}\:\mathrm{36}{km}/{h}. \\ $$$${Two}\:{cars}\:{B}\:{and}\:{C}\:{approach}\:{A}\:{in} \\ $$$${opposite}\:{directions}\:{with}\:{a}\:{speed}\:{of} \\ $$$$\mathrm{54}{km}/{h}\:{each}.{At}\:{a}\:{certain}\:{instant}, \\ $$$${when}\:{the}\:{distance}\:{AB}\:{is}\:{equal} \\ $$$${to}\:{AC},{both}\:{being}\:\mathrm{1}{km},{B}\:{decides} \\ $$$${to}\:{overtake}\:{A}\:{before}\:{C}\:{does}.{What} \\ $$$${minimum}\:{acceleration}\:{of}\:{carB} \\ $$$${is}\:{required}\:{to}\:{avoid}\:{an}\:{accident}? \\ $$

Question Number 29354 Answers: 2 Comments: 0

3sin^2 θ −sin θcos θ −4cos^2 θ=0 find the values of θ if θ lies between 0 and 360

$$\mathrm{3sin}\:^{\mathrm{2}} \theta\:−\mathrm{sin}\:\theta\mathrm{cos}\:\theta\:−\mathrm{4cos}\:^{\mathrm{2}} \theta=\mathrm{0} \\ $$$${find}\:{the}\:{values}\:{of}\:\theta\:{if}\:\theta\:{lies} \\ $$$${between}\:\mathrm{0}\:{and}\:\mathrm{360} \\ $$

Question Number 29349 Answers: 0 Comments: 1

let give f(x)= (x^n −1) e^(−x) with n from N^★ find f^((n)) (0) .

$${let}\:{give}\:{f}\left({x}\right)=\:\left({x}^{{n}} −\mathrm{1}\right)\:{e}^{−{x}} \:\:{with}\:{n}\:{from}\:{N}^{\bigstar} \: \\ $$$${find}\:{f}^{\left({n}\right)} \left(\mathrm{0}\right)\:. \\ $$

Question Number 29347 Answers: 0 Comments: 0

y^((1)) +((2/(xln x))+(((1−4x^2 ln x))/(x(1−2xln x))))y=0

$${y}^{\left(\mathrm{1}\right)} +\left(\frac{\mathrm{2}}{{x}\mathrm{ln}\:{x}}+\frac{\left(\mathrm{1}−\mathrm{4}{x}^{\mathrm{2}} \mathrm{ln}\:{x}\right)}{{x}\left(\mathrm{1}−\mathrm{2}{x}\mathrm{ln}\:{x}\right)}\right){y}=\mathrm{0} \\ $$

Question Number 29345 Answers: 1 Comments: 0

solve simultanrodly x+y=5.....(1) x^y +y^x =17.....(2)

$$\mathrm{solve}\:\mathrm{simultanrodly} \\ $$$$ \\ $$$$\mathrm{x}+\mathrm{y}=\mathrm{5}.....\left(\mathrm{1}\right) \\ $$$$\mathrm{x}^{\mathrm{y}} +\mathrm{y}^{\mathrm{x}} =\mathrm{17}.....\left(\mathrm{2}\right) \\ $$

Question Number 29423 Answers: 0 Comments: 1

Question Number 29332 Answers: 1 Comments: 0

Question Number 29326 Answers: 1 Comments: 0

The unit digit of the square of a number and the units digit of the cube of the number are equal to the unit digit of the number. How many values are possible for the units digits of such numbers?

$$\mathrm{The}\:\mathrm{unit}\:\mathrm{digit}\:\mathrm{of}\:\mathrm{the}\:\mathrm{square}\:\mathrm{of}\:\mathrm{a}\:\mathrm{number} \\ $$$$\mathrm{and}\:\mathrm{the}\:\mathrm{units}\:\mathrm{digit}\:\mathrm{of}\:\mathrm{the}\:\mathrm{cube}\:\mathrm{of}\:\mathrm{the}\: \\ $$$$\mathrm{number}\:\mathrm{are}\:\mathrm{equal}\:\mathrm{to}\:\mathrm{the}\:\mathrm{unit}\:\mathrm{digit}\:\mathrm{of} \\ $$$$\mathrm{the}\:\mathrm{number}.\:\mathrm{How}\:\mathrm{many}\:\mathrm{values}\:\mathrm{are}\: \\ $$$$\mathrm{possible}\:\mathrm{for}\:\mathrm{the}\:\mathrm{units}\:\mathrm{digits}\:\mathrm{of}\:\mathrm{such} \\ $$$$\mathrm{numbers}? \\ $$

Question Number 29324 Answers: 1 Comments: 0