
AllQuestion and Answers: Page 1789
Question Number 31041 Answers: 0 Comments: 0
$${solve}\:{in}\:{Z}^{\mathrm{2}} \:\mathrm{11}{x}\:−\mathrm{5}{y}\:=\mathrm{14} \\ $$
Question Number 31040 Answers: 0 Comments: 0
$${solve}\:{in}\:{Z}^{\mathrm{2}} \:{x}^{\mathrm{2}} \:−{y}^{\mathrm{2}} =\mathrm{1969} \\ $$
Question Number 31039 Answers: 0 Comments: 0
Question Number 31038 Answers: 0 Comments: 0
Question Number 31037 Answers: 0 Comments: 0
Question Number 31036 Answers: 0 Comments: 0
$${solve}\:{inside}\:{C}\:\:{z}^{\mathrm{6}} =\:\left({z}^{−} \right)^{\mathrm{2}} \:\:. \\ $$
Question Number 31035 Answers: 0 Comments: 0
Question Number 31034 Answers: 0 Comments: 0
Question Number 31033 Answers: 0 Comments: 0
Question Number 31032 Answers: 0 Comments: 0
Question Number 31031 Answers: 0 Comments: 0
Question Number 31030 Answers: 0 Comments: 0
Question Number 31029 Answers: 0 Comments: 1

Question Number 31026 Answers: 0 Comments: 2
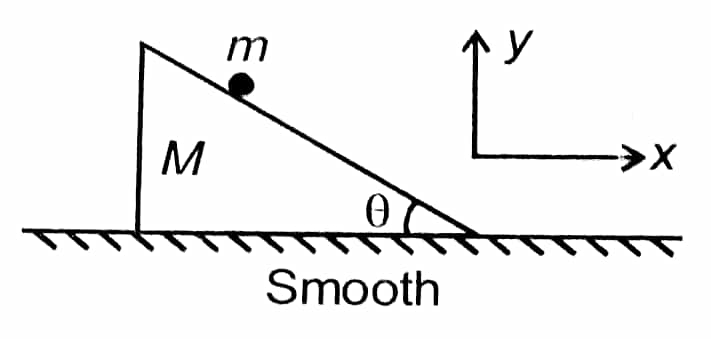
Question Number 31023 Answers: 0 Comments: 0

Question Number 31018 Answers: 0 Comments: 1

Question Number 31016 Answers: 1 Comments: 0
Question Number 31017 Answers: 1 Comments: 0
Question Number 31148 Answers: 1 Comments: 1
Question Number 31147 Answers: 1 Comments: 0
Question Number 31145 Answers: 1 Comments: 0
Question Number 31144 Answers: 0 Comments: 2
Question Number 31143 Answers: 1 Comments: 0
Question Number 31141 Answers: 1 Comments: 0
Question Number 31004 Answers: 1 Comments: 0
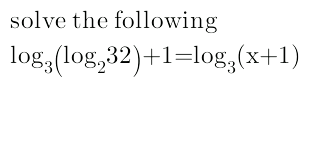
Question Number 31003 Answers: 1 Comments: 0
Pg 1784 Pg 1785 Pg 1786 Pg 1787 Pg 1788 Pg 1789 Pg 1790 Pg 1791 Pg 1792 Pg 1793
