
AllQuestion and Answers: Page 1778
Question Number 32266 Answers: 0 Comments: 0

Question Number 32264 Answers: 0 Comments: 1
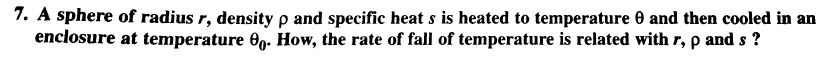
Question Number 32258 Answers: 2 Comments: 0
$${find} \\ $$$$\int\:\frac{\mathrm{1}}{\mathrm{2}−{x}^{\mathrm{2}} }\:{dx} \\ $$
Question Number 32256 Answers: 0 Comments: 0
Question Number 32255 Answers: 0 Comments: 0
Question Number 32265 Answers: 0 Comments: 0

Question Number 32242 Answers: 1 Comments: 0
Question Number 32241 Answers: 0 Comments: 1

Question Number 32240 Answers: 1 Comments: 0
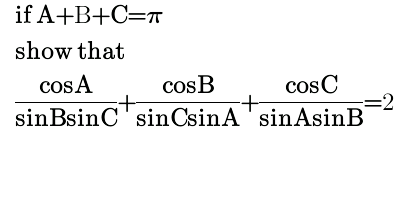
Question Number 32239 Answers: 1 Comments: 0
Question Number 32237 Answers: 0 Comments: 0

Question Number 32236 Answers: 1 Comments: 0

Question Number 32233 Answers: 0 Comments: 1
Question Number 32220 Answers: 0 Comments: 3
Question Number 32218 Answers: 1 Comments: 0

Question Number 32209 Answers: 1 Comments: 0
Question Number 32208 Answers: 0 Comments: 0

Question Number 32207 Answers: 0 Comments: 0
Question Number 32206 Answers: 0 Comments: 0
Question Number 32203 Answers: 0 Comments: 5
Question Number 32191 Answers: 1 Comments: 1
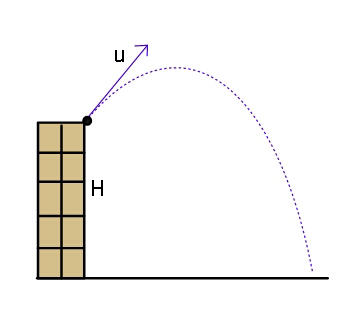
Question Number 32211 Answers: 1 Comments: 1
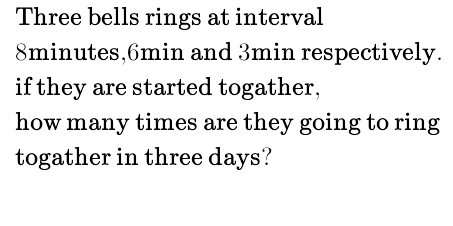
Question Number 32184 Answers: 1 Comments: 0
Question Number 32181 Answers: 1 Comments: 1
Question Number 32163 Answers: 0 Comments: 0
Question Number 32161 Answers: 1 Comments: 0
Pg 1773 Pg 1774 Pg 1775 Pg 1776 Pg 1777 Pg 1778 Pg 1779 Pg 1780 Pg 1781 Pg 1782
