
AllQuestion and Answers: Page 1777
Question Number 32294 Answers: 0 Comments: 1
Question Number 32293 Answers: 1 Comments: 1
Question Number 32291 Answers: 0 Comments: 0
Question Number 32290 Answers: 0 Comments: 1
Question Number 32289 Answers: 0 Comments: 0
Question Number 32288 Answers: 0 Comments: 0
Question Number 32287 Answers: 0 Comments: 0
Question Number 32286 Answers: 0 Comments: 0
Question Number 32281 Answers: 0 Comments: 0
Question Number 32280 Answers: 0 Comments: 0
Question Number 32279 Answers: 0 Comments: 0
Question Number 32282 Answers: 0 Comments: 0
Question Number 32278 Answers: 0 Comments: 0
Question Number 32277 Answers: 0 Comments: 0
Question Number 32276 Answers: 0 Comments: 0
Question Number 32285 Answers: 0 Comments: 0
Question Number 32284 Answers: 0 Comments: 0
Question Number 32283 Answers: 1 Comments: 1
Question Number 32274 Answers: 0 Comments: 0
Question Number 32273 Answers: 1 Comments: 1
Question Number 32271 Answers: 0 Comments: 0
Question Number 32269 Answers: 1 Comments: 0
$${find}\:\int\:\:\frac{{x}^{\mathrm{3}} }{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\:{dx} \\ $$
Question Number 32266 Answers: 0 Comments: 0

Question Number 32264 Answers: 0 Comments: 1
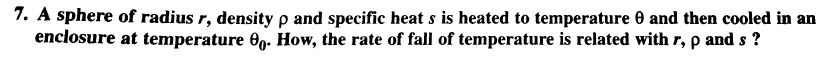
Question Number 32258 Answers: 2 Comments: 0
$${find} \\ $$$$\int\:\frac{\mathrm{1}}{\mathrm{2}−{x}^{\mathrm{2}} }\:{dx} \\ $$
Question Number 32256 Answers: 0 Comments: 0
Pg 1772 Pg 1773 Pg 1774 Pg 1775 Pg 1776 Pg 1777 Pg 1778 Pg 1779 Pg 1780 Pg 1781
