
AllQuestion and Answers: Page 1774
Question Number 32473 Answers: 0 Comments: 0

Question Number 32472 Answers: 0 Comments: 0

Question Number 32471 Answers: 0 Comments: 0

Question Number 32470 Answers: 0 Comments: 0
Question Number 32458 Answers: 0 Comments: 0
Question Number 32446 Answers: 1 Comments: 0
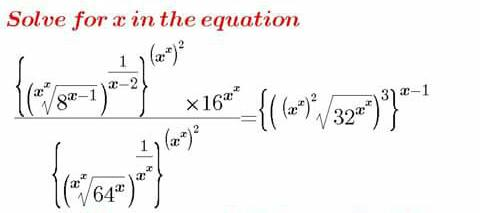
Question Number 32444 Answers: 0 Comments: 6

Question Number 32441 Answers: 1 Comments: 0

Question Number 32440 Answers: 1 Comments: 0

Question Number 32524 Answers: 0 Comments: 0
$$\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} +\sqrt{\mathrm{2}}= \\ $$
Question Number 32425 Answers: 0 Comments: 0
Question Number 32424 Answers: 1 Comments: 0

Question Number 32423 Answers: 0 Comments: 0

Question Number 32420 Answers: 0 Comments: 0
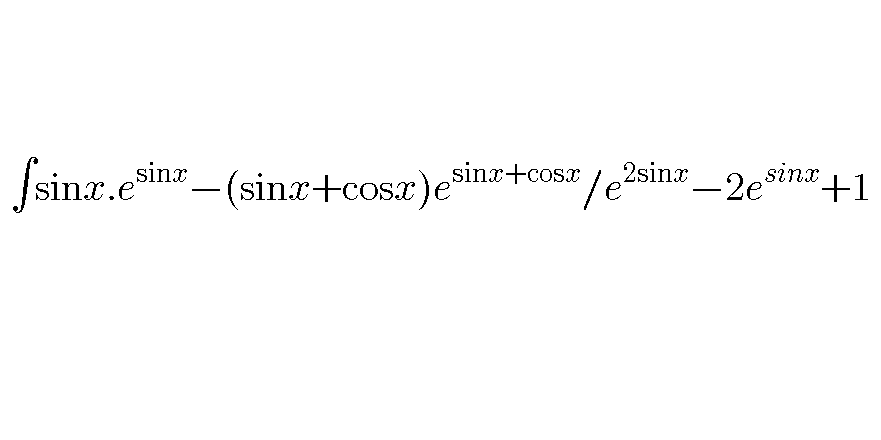
Question Number 32419 Answers: 0 Comments: 0
Question Number 32418 Answers: 0 Comments: 1
Question Number 32409 Answers: 1 Comments: 0

Question Number 32407 Answers: 0 Comments: 1
Question Number 32402 Answers: 0 Comments: 1
Question Number 32401 Answers: 0 Comments: 0
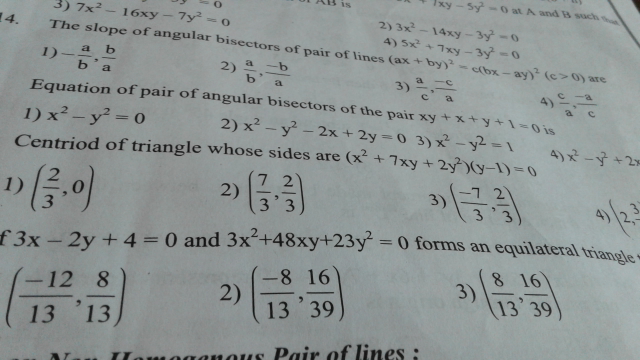
Question Number 32399 Answers: 0 Comments: 0
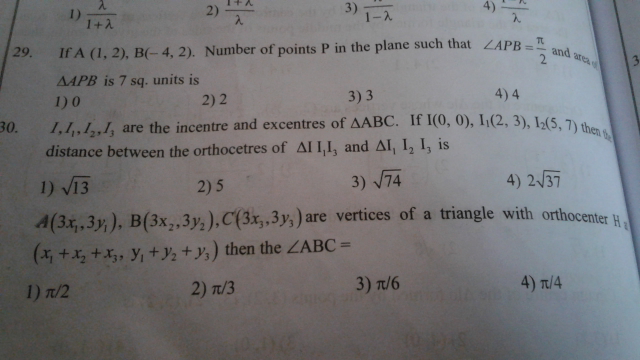
Question Number 32396 Answers: 1 Comments: 0
$${roots} \\ $$$$\mathrm{2}{x}×\boldsymbol{{x}}+\boldsymbol{{x}}+\mathrm{3} \\ $$
Question Number 32395 Answers: 0 Comments: 1
Question Number 32382 Answers: 2 Comments: 2
Question Number 32380 Answers: 1 Comments: 2
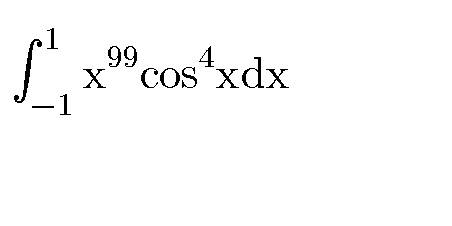
Question Number 32379 Answers: 1 Comments: 0

Pg 1769 Pg 1770 Pg 1771 Pg 1772 Pg 1773 Pg 1774 Pg 1775 Pg 1776 Pg 1777 Pg 1778
