
AllQuestion and Answers: Page 1769
Question Number 32872 Answers: 1 Comments: 0

Question Number 32870 Answers: 0 Comments: 0
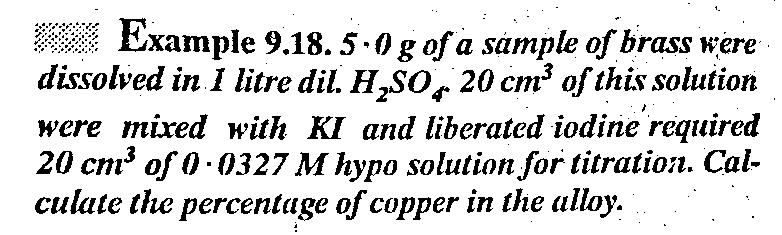
Question Number 32869 Answers: 1 Comments: 1
Question Number 32850 Answers: 0 Comments: 1
$${evaluate} \\ $$$$\int_{\mathrm{0}} ^{\pi} \mathrm{42}\left(\mathrm{2}\right){dx} \\ $$
Question Number 32868 Answers: 0 Comments: 0
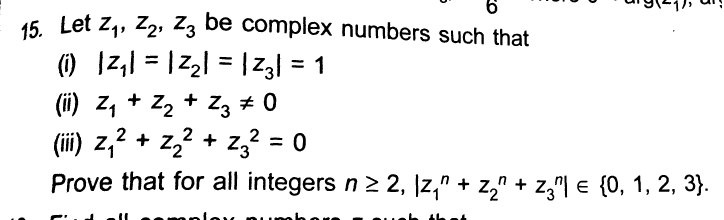
Question Number 32845 Answers: 1 Comments: 0
Question Number 32844 Answers: 0 Comments: 1
Question Number 32841 Answers: 1 Comments: 0
Question Number 32837 Answers: 0 Comments: 1
Question Number 32838 Answers: 2 Comments: 2
Question Number 32834 Answers: 1 Comments: 0
Question Number 32832 Answers: 0 Comments: 0
Question Number 32830 Answers: 0 Comments: 0
Question Number 32810 Answers: 1 Comments: 2
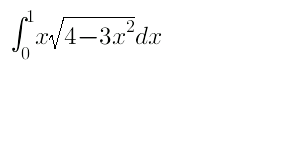
Question Number 33004 Answers: 0 Comments: 3
Question Number 32965 Answers: 0 Comments: 2

Question Number 32960 Answers: 1 Comments: 0
Question Number 32789 Answers: 0 Comments: 0
Question Number 32788 Answers: 0 Comments: 1
Question Number 32785 Answers: 1 Comments: 0
Question Number 32780 Answers: 2 Comments: 0
Question Number 32776 Answers: 1 Comments: 0
Question Number 32775 Answers: 1 Comments: 0
Question Number 32768 Answers: 1 Comments: 0
Question Number 32767 Answers: 0 Comments: 2
Question Number 32765 Answers: 0 Comments: 0

Pg 1764 Pg 1765 Pg 1766 Pg 1767 Pg 1768 Pg 1769 Pg 1770 Pg 1771 Pg 1772 Pg 1773
