
AllQuestion and Answers: Page 1768
Question Number 32954 Answers: 1 Comments: 0
Question Number 32951 Answers: 2 Comments: 1
Question Number 32947 Answers: 1 Comments: 0
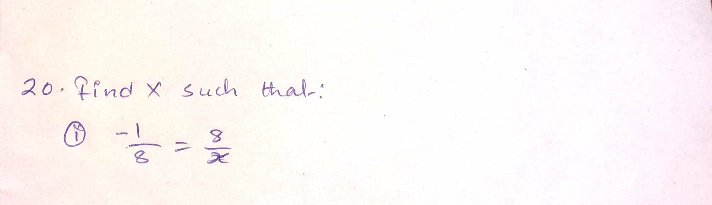
Question Number 32946 Answers: 1 Comments: 0

Question Number 32945 Answers: 1 Comments: 0
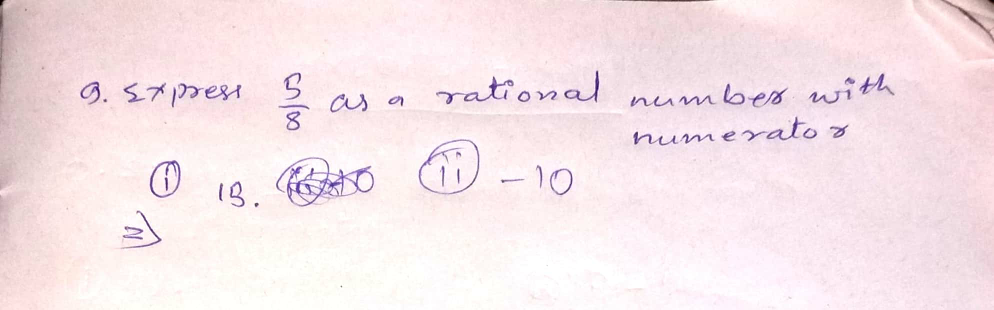
Question Number 32939 Answers: 1 Comments: 1
Question Number 32938 Answers: 0 Comments: 2
Question Number 32937 Answers: 0 Comments: 0
Question Number 32936 Answers: 0 Comments: 0
Question Number 32935 Answers: 0 Comments: 0
Question Number 32934 Answers: 0 Comments: 0
Question Number 32933 Answers: 0 Comments: 0
Question Number 32932 Answers: 0 Comments: 1
Question Number 32928 Answers: 2 Comments: 2
Question Number 32918 Answers: 0 Comments: 1
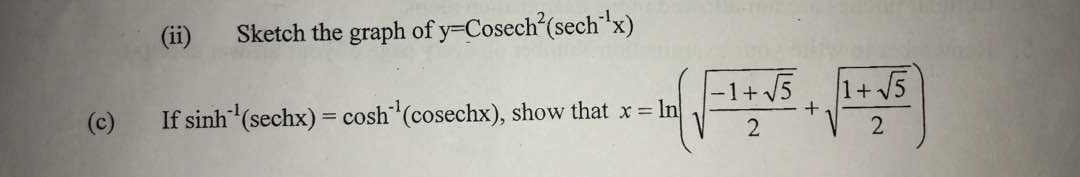
Question Number 32914 Answers: 0 Comments: 4

Question Number 32913 Answers: 0 Comments: 0
Question Number 32912 Answers: 1 Comments: 0
Question Number 32908 Answers: 2 Comments: 2
Question Number 32900 Answers: 0 Comments: 0

Question Number 32897 Answers: 3 Comments: 0
$$ \\ $$$${e}^{\pi} \:>\:\pi^{{e}} \:\:{or}\:\:\:{e}^{\pi} <\pi^{{e}} \:? \\ $$$$ \\ $$
Question Number 32891 Answers: 0 Comments: 3
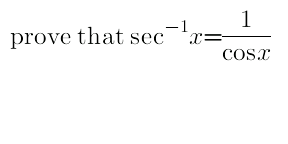
Question Number 32889 Answers: 0 Comments: 1

Question Number 32885 Answers: 1 Comments: 0

Question Number 32878 Answers: 1 Comments: 0
Question Number 32877 Answers: 1 Comments: 0
Pg 1763 Pg 1764 Pg 1765 Pg 1766 Pg 1767 Pg 1768 Pg 1769 Pg 1770 Pg 1771 Pg 1772
