
AllQuestion and Answers: Page 1764
Question Number 33239 Answers: 1 Comments: 0

Question Number 33230 Answers: 1 Comments: 0
Question Number 33222 Answers: 0 Comments: 0
Question Number 33223 Answers: 0 Comments: 0
Question Number 33218 Answers: 1 Comments: 0
Question Number 33217 Answers: 0 Comments: 7

Question Number 33216 Answers: 1 Comments: 0

Question Number 33214 Answers: 0 Comments: 8

Question Number 33211 Answers: 0 Comments: 0
Question Number 33210 Answers: 0 Comments: 0
Question Number 33209 Answers: 0 Comments: 0
Question Number 33208 Answers: 0 Comments: 0
Question Number 33207 Answers: 0 Comments: 0

Question Number 33204 Answers: 0 Comments: 1
Question Number 33232 Answers: 0 Comments: 1
Question Number 33200 Answers: 1 Comments: 0
Question Number 33199 Answers: 0 Comments: 1
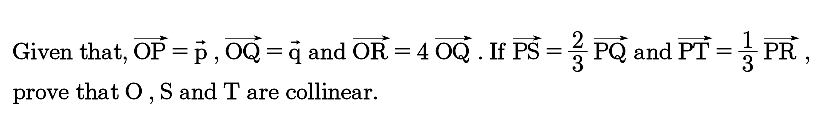
Question Number 33195 Answers: 0 Comments: 0

Question Number 33193 Answers: 1 Comments: 0
Question Number 33186 Answers: 1 Comments: 0
Question Number 33185 Answers: 1 Comments: 0
Question Number 33184 Answers: 0 Comments: 0
Question Number 33202 Answers: 0 Comments: 1
Question Number 33175 Answers: 0 Comments: 1
Question Number 33174 Answers: 0 Comments: 0
Question Number 33173 Answers: 0 Comments: 0
Pg 1759 Pg 1760 Pg 1761 Pg 1762 Pg 1763 Pg 1764 Pg 1765 Pg 1766 Pg 1767 Pg 1768
