
AllQuestion and Answers: Page 1756
Question Number 33531 Answers: 0 Comments: 16
Question Number 33518 Answers: 0 Comments: 0
$$\alpha^{\mathrm{4}} +\beta^{\mathrm{4}\:} {solve}\:{please} \\ $$
Question Number 33515 Answers: 0 Comments: 1
$${expand}\:\alpha^{\mathrm{4}} +\beta^{\beta\:\:} {please} \\ $$
Question Number 33513 Answers: 0 Comments: 1
Question Number 33511 Answers: 1 Comments: 0
Question Number 33508 Answers: 0 Comments: 2
$$\frac{\mathrm{3}^{{x}} ×\mathrm{8}^{{x}} }{\mathrm{12}^{{x}+\mathrm{1}} } \\ $$
Question Number 33507 Answers: 1 Comments: 0
$$\int\frac{\mathrm{2cos}\:{x}}{\mathrm{3}−\mathrm{cos}\:\mathrm{2}{x}}{dx}=? \\ $$
Question Number 33496 Answers: 1 Comments: 0
$$\mathrm{prove}\:\mathrm{that} \\ $$$$\mathrm{e}^{\mathrm{i}\pi} +\mathrm{1}=\mathrm{0} \\ $$
Question Number 33494 Answers: 0 Comments: 2
Question Number 33473 Answers: 1 Comments: 3
Question Number 33479 Answers: 2 Comments: 2
Question Number 33468 Answers: 1 Comments: 0
Question Number 33466 Answers: 1 Comments: 2
Question Number 33463 Answers: 0 Comments: 1
Question Number 33462 Answers: 1 Comments: 0
Question Number 33460 Answers: 1 Comments: 0
Question Number 33455 Answers: 1 Comments: 2
Question Number 33452 Answers: 1 Comments: 2
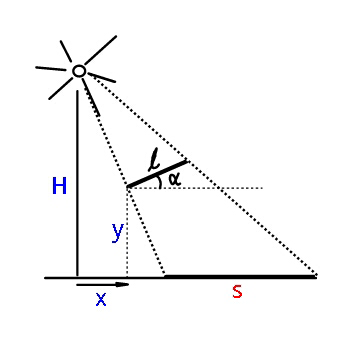
Question Number 33435 Answers: 1 Comments: 0
Question Number 33430 Answers: 0 Comments: 3
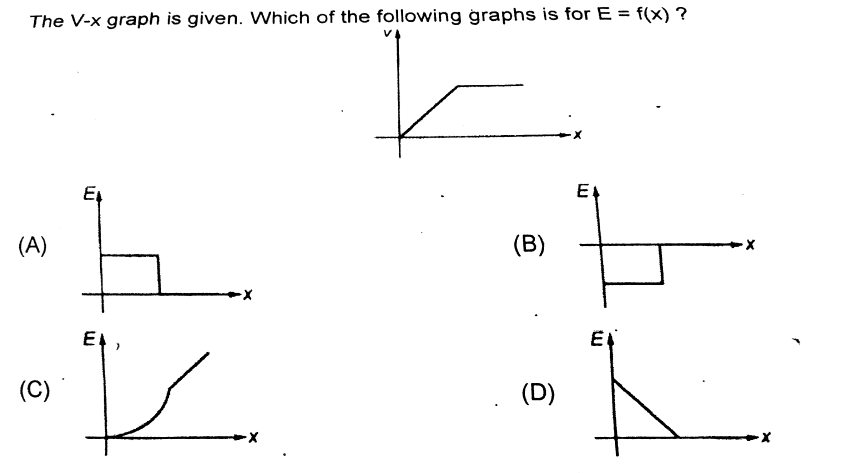
Question Number 33425 Answers: 1 Comments: 3
Question Number 33413 Answers: 0 Comments: 2
Question Number 33411 Answers: 0 Comments: 1
Question Number 33410 Answers: 1 Comments: 1
Question Number 33407 Answers: 1 Comments: 0
Question Number 33406 Answers: 0 Comments: 4
$${Find}\:{the}\:{half}\:{derivative}\:{of}\:{y}=\mathrm{ln}\:{x} \\ $$
Pg 1751 Pg 1752 Pg 1753 Pg 1754 Pg 1755 Pg 1756 Pg 1757 Pg 1758 Pg 1759 Pg 1760
