
AllQuestion and Answers: Page 1755
Question Number 33942 Answers: 1 Comments: 1
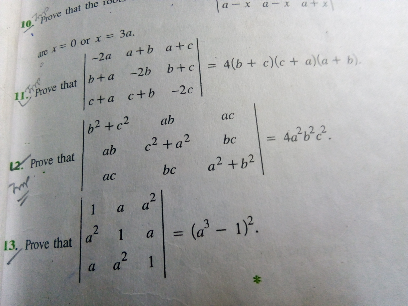
Question Number 33941 Answers: 0 Comments: 0
Question Number 33940 Answers: 3 Comments: 0
Question Number 33930 Answers: 1 Comments: 0
Question Number 33927 Answers: 0 Comments: 6

Question Number 33926 Answers: 0 Comments: 0
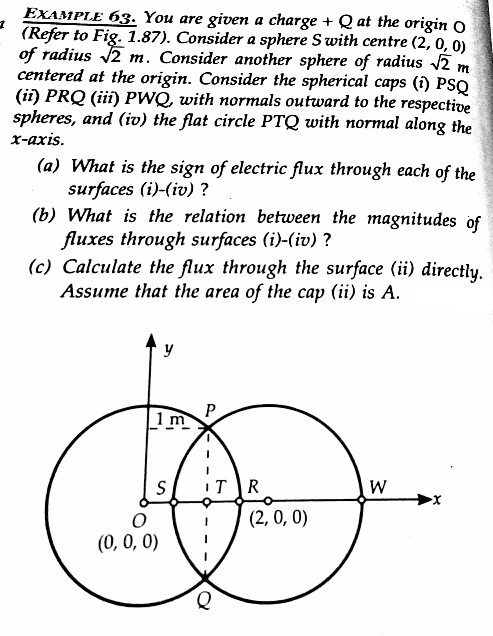
Question Number 33915 Answers: 2 Comments: 3
Question Number 33912 Answers: 0 Comments: 3

Question Number 33907 Answers: 0 Comments: 1

Question Number 33899 Answers: 2 Comments: 0
Question Number 33897 Answers: 2 Comments: 0
Question Number 33896 Answers: 3 Comments: 0
Question Number 33895 Answers: 3 Comments: 0
Question Number 33894 Answers: 0 Comments: 1
Question Number 33892 Answers: 0 Comments: 1
Question Number 33891 Answers: 0 Comments: 1
Question Number 33890 Answers: 0 Comments: 0
Question Number 33889 Answers: 0 Comments: 0
Question Number 33888 Answers: 0 Comments: 0
Question Number 33887 Answers: 0 Comments: 0
Question Number 33886 Answers: 0 Comments: 1
Question Number 33885 Answers: 0 Comments: 1
Question Number 33884 Answers: 0 Comments: 1
Question Number 33883 Answers: 0 Comments: 1
Question Number 33867 Answers: 1 Comments: 0
Question Number 33865 Answers: 0 Comments: 2
Pg 1750 Pg 1751 Pg 1752 Pg 1753 Pg 1754 Pg 1755 Pg 1756 Pg 1757 Pg 1758 Pg 1759
