
AllQuestion and Answers: Page 1754
Question Number 31369 Answers: 0 Comments: 0

Question Number 31350 Answers: 0 Comments: 0
Question Number 31340 Answers: 0 Comments: 0
Question Number 31336 Answers: 0 Comments: 1
Question Number 31335 Answers: 0 Comments: 3
$${Find}\:{the}\:{pricipal}\:{value}\:{of}\: \\ $$$${z}=\left(\mathrm{1}−{i}\right)^{{i}} \\ $$
Question Number 31329 Answers: 0 Comments: 5

Question Number 31327 Answers: 0 Comments: 1
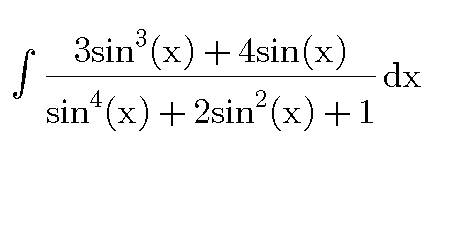
Question Number 31326 Answers: 1 Comments: 1

Question Number 31324 Answers: 1 Comments: 0

Question Number 31323 Answers: 1 Comments: 0

Question Number 31320 Answers: 1 Comments: 0
Question Number 31318 Answers: 1 Comments: 1

Question Number 31317 Answers: 0 Comments: 1

Question Number 31314 Answers: 0 Comments: 0
Question Number 31306 Answers: 1 Comments: 0
Question Number 31296 Answers: 0 Comments: 11
Question Number 31295 Answers: 0 Comments: 0

Question Number 31289 Answers: 1 Comments: 0

Question Number 31287 Answers: 0 Comments: 0
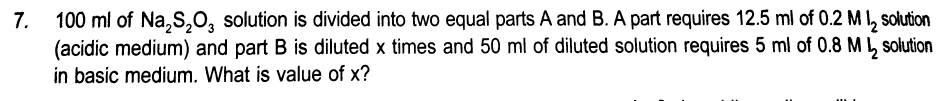
Question Number 31286 Answers: 1 Comments: 1
Question Number 31284 Answers: 0 Comments: 0
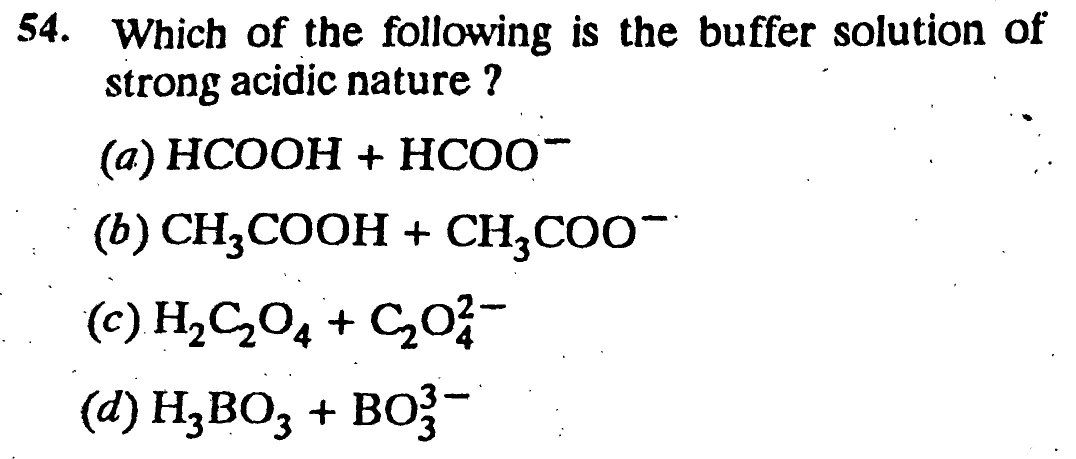
Question Number 31281 Answers: 1 Comments: 0
Question Number 31265 Answers: 0 Comments: 2

Question Number 31264 Answers: 0 Comments: 2
Question Number 31292 Answers: 1 Comments: 3

Question Number 31290 Answers: 1 Comments: 1

Pg 1749 Pg 1750 Pg 1751 Pg 1752 Pg 1753 Pg 1754 Pg 1755 Pg 1756 Pg 1757 Pg 1758
