
AllQuestion and Answers: Page 1753
Question Number 34160 Answers: 1 Comments: 3
Question Number 34159 Answers: 1 Comments: 1
Question Number 34142 Answers: 0 Comments: 1
Question Number 34140 Answers: 2 Comments: 0
Question Number 34139 Answers: 2 Comments: 0
Question Number 34129 Answers: 2 Comments: 2
Question Number 34126 Answers: 0 Comments: 0
Question Number 34119 Answers: 3 Comments: 0
Question Number 34117 Answers: 0 Comments: 1

Question Number 34116 Answers: 0 Comments: 1

Question Number 34110 Answers: 0 Comments: 2

Question Number 34109 Answers: 0 Comments: 0

Question Number 34107 Answers: 0 Comments: 6

Question Number 34114 Answers: 0 Comments: 0
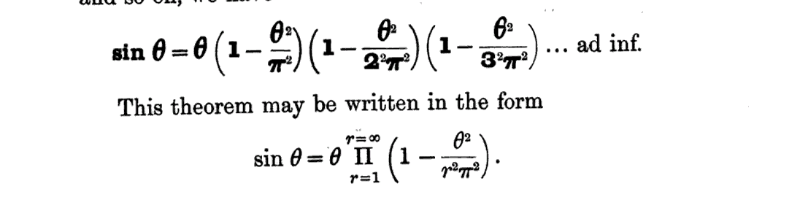
Question Number 34113 Answers: 0 Comments: 0
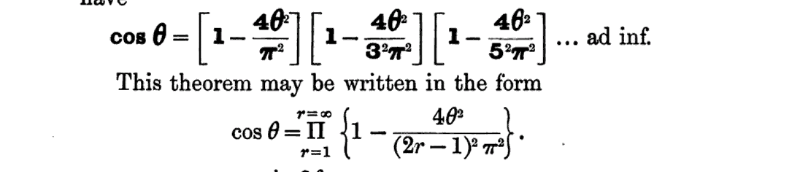
Question Number 34115 Answers: 0 Comments: 1

Question Number 34095 Answers: 0 Comments: 0

Question Number 34094 Answers: 0 Comments: 2

Question Number 34092 Answers: 2 Comments: 9
Question Number 34098 Answers: 0 Comments: 13
Question Number 34081 Answers: 1 Comments: 0
$$\mathrm{2}^{{n}} −\mathrm{2}^{{n}−\mathrm{1}} =\mathrm{4}\:.{find}\:{n}^{{n}.} \\ $$
Question Number 34066 Answers: 1 Comments: 0
Question Number 34064 Answers: 1 Comments: 0

Question Number 34056 Answers: 2 Comments: 3
Question Number 34051 Answers: 1 Comments: 0
$$\mathrm{2}{dy}/{dx}+{y}=\mathrm{0}\:\:{y}\left(\mathrm{0}\right)=−\mathrm{3} \\ $$
Question Number 34044 Answers: 2 Comments: 2
Pg 1748 Pg 1749 Pg 1750 Pg 1751 Pg 1752 Pg 1753 Pg 1754 Pg 1755 Pg 1756 Pg 1757
