
AllQuestion and Answers: Page 1747
Question Number 34647 Answers: 2 Comments: 0
Question Number 34646 Answers: 1 Comments: 0
Question Number 34645 Answers: 0 Comments: 0
Question Number 34639 Answers: 2 Comments: 0

Question Number 34635 Answers: 2 Comments: 4
Question Number 34634 Answers: 1 Comments: 1
Question Number 34633 Answers: 0 Comments: 0
Question Number 34632 Answers: 0 Comments: 0
Question Number 34617 Answers: 2 Comments: 2

Question Number 34615 Answers: 0 Comments: 0
Question Number 34608 Answers: 0 Comments: 0

Question Number 34607 Answers: 0 Comments: 0
Question Number 34606 Answers: 0 Comments: 0
Question Number 34605 Answers: 0 Comments: 0
Question Number 34604 Answers: 0 Comments: 0
Question Number 34603 Answers: 0 Comments: 0
Question Number 34602 Answers: 0 Comments: 0
Question Number 34596 Answers: 0 Comments: 0
Question Number 34595 Answers: 0 Comments: 0
Question Number 34594 Answers: 0 Comments: 0
Question Number 34593 Answers: 0 Comments: 0
Question Number 34587 Answers: 2 Comments: 1
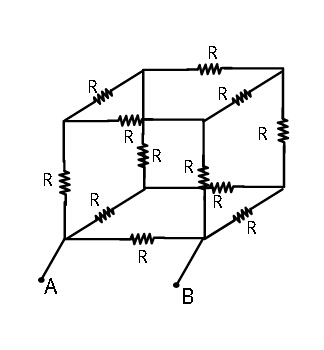
Question Number 34585 Answers: 1 Comments: 1
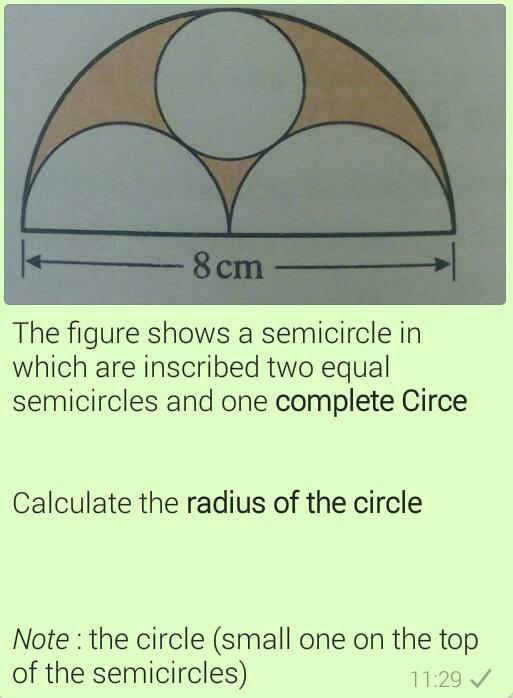
Question Number 34571 Answers: 0 Comments: 0
Question Number 34567 Answers: 1 Comments: 0
$${x}\begin{vmatrix}{\mathrm{2}}\\{}\end{vmatrix}−\mathrm{2}{x}−\mathrm{15}=\mathrm{0} \\ $$
Question Number 34562 Answers: 1 Comments: 1
Pg 1742 Pg 1743 Pg 1744 Pg 1745 Pg 1746 Pg 1747 Pg 1748 Pg 1749 Pg 1750 Pg 1751
