
AllQuestion and Answers: Page 1741
Question Number 35051 Answers: 0 Comments: 1
Question Number 35050 Answers: 0 Comments: 0
Question Number 35049 Answers: 1 Comments: 1
Question Number 35048 Answers: 0 Comments: 0
$${find}\:\int\:\:\:\:\:\frac{{dx}}{{cos}\left({sinx}\right)} \\ $$
Question Number 35046 Answers: 0 Comments: 0
Question Number 35045 Answers: 0 Comments: 0
Question Number 35044 Answers: 1 Comments: 1
Question Number 35043 Answers: 1 Comments: 0
Question Number 35041 Answers: 0 Comments: 1
Question Number 35040 Answers: 0 Comments: 0
Question Number 35023 Answers: 1 Comments: 1

Question Number 35021 Answers: 0 Comments: 1
Question Number 35018 Answers: 1 Comments: 0
Question Number 35015 Answers: 2 Comments: 0
$$\int\frac{{x}^{\mathrm{2}} }{\left(\mathrm{1}+{x}^{\mathrm{3}} \right)^{\mathrm{2}} }{dx} \\ $$
Question Number 35005 Answers: 2 Comments: 0
Question Number 35004 Answers: 3 Comments: 0
Question Number 34992 Answers: 1 Comments: 1
Question Number 34988 Answers: 1 Comments: 1
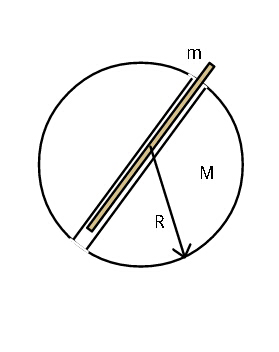
Question Number 34982 Answers: 2 Comments: 2
Question Number 34980 Answers: 2 Comments: 0
Question Number 34956 Answers: 3 Comments: 2

Question Number 34954 Answers: 1 Comments: 1
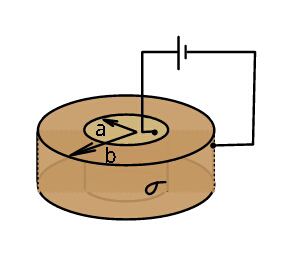
Question Number 34952 Answers: 0 Comments: 2
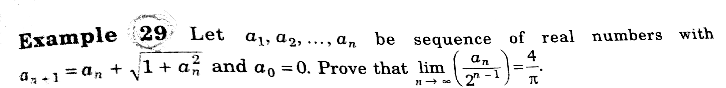
Question Number 34951 Answers: 1 Comments: 0
Question Number 34930 Answers: 1 Comments: 3
Question Number 34921 Answers: 1 Comments: 0
Pg 1736 Pg 1737 Pg 1738 Pg 1739 Pg 1740 Pg 1741 Pg 1742 Pg 1743 Pg 1744 Pg 1745
