
AllQuestion and Answers: Page 1739
Question Number 35338 Answers: 0 Comments: 1
Question Number 35336 Answers: 2 Comments: 1
$$\sqrt{\mathrm{2}{x}^{\mathrm{2}} }+\mathrm{7}{x}+\mathrm{5}\sqrt{\mathrm{2}}=\mathrm{0} \\ $$
Question Number 35325 Answers: 1 Comments: 0
Question Number 35419 Answers: 1 Comments: 0
Question Number 35313 Answers: 0 Comments: 0

Question Number 35304 Answers: 2 Comments: 4
Question Number 35300 Answers: 0 Comments: 0
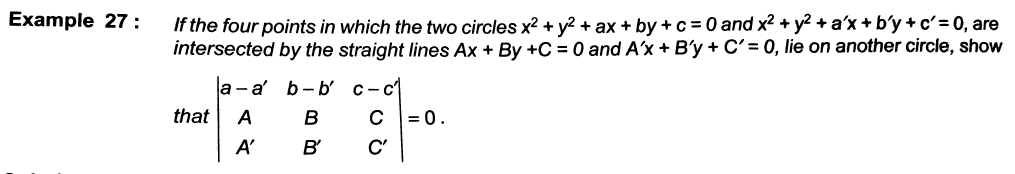
Question Number 35297 Answers: 0 Comments: 1
Question Number 35294 Answers: 1 Comments: 1
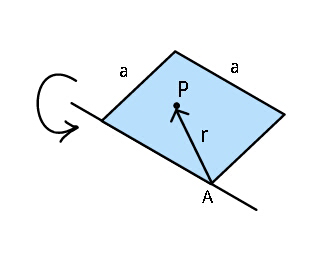
Question Number 35291 Answers: 1 Comments: 1
Question Number 35290 Answers: 0 Comments: 1
Question Number 35319 Answers: 2 Comments: 0

Question Number 35267 Answers: 1 Comments: 0

Question Number 35265 Answers: 0 Comments: 0
Question Number 35279 Answers: 0 Comments: 3
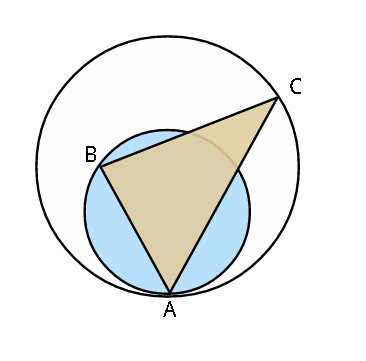
Question Number 35256 Answers: 1 Comments: 1
$$\mathrm{Factorize}\::\mathrm{x}^{\mathrm{5}} −\mathrm{y}^{\mathrm{5}} \\ $$
Question Number 35248 Answers: 0 Comments: 1

Question Number 35246 Answers: 1 Comments: 1
Question Number 35245 Answers: 0 Comments: 7
Question Number 35244 Answers: 0 Comments: 1
Question Number 35242 Answers: 1 Comments: 1
$${find}\:\:\int_{\mathrm{0}} ^{\pi} \:\:\:\:\frac{{xdx}}{\mathrm{1}+{sinx}} \\ $$
Question Number 35241 Answers: 2 Comments: 6
$${calculate}\:\int_{\mathrm{0}} ^{\pi} \:\:\:\:\frac{{x}\:{dx}}{\mathrm{3}\:+{cosx}}\:\:. \\ $$
Question Number 35238 Answers: 0 Comments: 1
Question Number 35237 Answers: 0 Comments: 1
Question Number 35236 Answers: 0 Comments: 0
Question Number 35235 Answers: 0 Comments: 2
Pg 1734 Pg 1735 Pg 1736 Pg 1737 Pg 1738 Pg 1739 Pg 1740 Pg 1741 Pg 1742 Pg 1743
