Question and Answers Forum

AllQuestion and Answers: Page 1736

Question Number 35061 Answers: 2 Comments: 1

find ∫_0 ^∞ ((x^2 +3)/((x^4 +1)^2 ))dx

$${find}\:\:\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\:\:\:\frac{{x}^{\mathrm{2}} \:+\mathrm{3}}{\left({x}^{\mathrm{4}} \:+\mathrm{1}\right)^{\mathrm{2}} }{dx} \\ $$

Question Number 35060 Answers: 1 Comments: 1

calculate ∫_0 ^(π/4) sinx ln(cosx)dx

$${calculate}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:{sinx}\:{ln}\left({cosx}\right){dx} \\ $$

Question Number 35059 Answers: 2 Comments: 2

find ∫_0 ^π (dx/(cosx +sinx))

$${find}\:\:\:\int_{\mathrm{0}} ^{\pi} \:\:\:\:\:\:\frac{{dx}}{{cosx}\:+{sinx}} \\ $$

Question Number 35058 Answers: 1 Comments: 1

find ∫_0 ^(π/4) (dt/((1+cos^2 t)^3 ))

$${find}\:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\:\:\frac{{dt}}{\left(\mathrm{1}+{cos}^{\mathrm{2}} {t}\right)^{\mathrm{3}} } \\ $$

Question Number 35057 Answers: 0 Comments: 1

let u_n =((n/(n+1)))^(1/n) −1 find the nature of Σ_(n≥0) u_n

$${let}\:{u}_{{n}} =\left(\frac{{n}}{{n}+\mathrm{1}}\right)^{\frac{\mathrm{1}}{{n}}} \:\:−\mathrm{1} \\ $$$${find}\:{the}\:{nature}\:{of}\:\sum_{{n}\geqslant\mathrm{0}} {u}_{{n}} \\ $$

Question Number 35056 Answers: 0 Comments: 2

let p(x)=(1+jx)^n −(1−jx)^n 1) find the roots of p(x) 2)factorize p(x) inside C[x] j =e^(i((2π)/3)) .

$${let}\:{p}\left({x}\right)=\left(\mathrm{1}+{jx}\right)^{{n}} \:−\left(\mathrm{1}−{jx}\right)^{{n}} \\ $$$$\left.\mathrm{1}\right)\:{find}\:{the}\:{roots}\:{of}\:{p}\left({x}\right) \\ $$$$\left.\mathrm{2}\right){factorize}\:{p}\left({x}\right)\:{inside}\:{C}\left[{x}\right] \\ $$$${j}\:={e}^{{i}\frac{\mathrm{2}\pi}{\mathrm{3}}} \:. \\ $$

Question Number 35055 Answers: 1 Comments: 2

calculate ∫_(−∞) ^(+∞) (dx/((1+x+x^2 )^3 ))

$${calculate}\:\int_{−\infty} ^{+\infty} \:\:\:\:\:\frac{{dx}}{\left(\mathrm{1}+{x}+{x}^{\mathrm{2}} \right)^{\mathrm{3}} } \\ $$

Question Number 35054 Answers: 0 Comments: 1

find ∫_0 ^(π/4) ((xdx)/(2 +cosx))

$${find}\:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\:\:\frac{{xdx}}{\mathrm{2}\:+{cosx}} \\ $$

Question Number 35053 Answers: 0 Comments: 0

let v(x)=ln(1+x+x^2 ) developp f at integr serie.

$${let}\:{v}\left({x}\right)={ln}\left(\mathrm{1}+{x}+{x}^{\mathrm{2}} \right) \\ $$$${developp}\:{f}\:{at}\:{integr}\:{serie}. \\ $$

Question Number 35052 Answers: 0 Comments: 1

let f(x) = (x/(x^2 +x−1)) developp f atintegr serie

$${let}\:{f}\left({x}\right)\:=\:\:\frac{{x}}{{x}^{\mathrm{2}} \:+{x}−\mathrm{1}} \\ $$$${developp}\:{f}\:{atintegr}\:{serie} \\ $$

Question Number 35051 Answers: 0 Comments: 1

calculate Σ_(n=0) ^∞ ((n+3)/(2n+1))x^n

$${calculate}\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{{n}+\mathrm{3}}{\mathrm{2}{n}+\mathrm{1}}{x}^{{n}} \\ $$$$ \\ $$

Question Number 35050 Answers: 0 Comments: 0

calculate Σ_(n=0) ^∞ (((−1)^n x^(2n+1) )/(4n^2 −1))

$${calculate}\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\:\frac{\left(−\mathrm{1}\right)^{{n}} \:\:{x}^{\mathrm{2}{n}+\mathrm{1}} }{\mathrm{4}{n}^{\mathrm{2}} −\mathrm{1}} \\ $$

Question Number 35049 Answers: 1 Comments: 1

let A_n = ∫_(1/n) ^n (1+(1/x^2 ))arctanx dx 1) calculate A_n 2) find lim_(n→+∞) A_n

$${let}\:{A}_{{n}} \:=\:\int_{\frac{\mathrm{1}}{{n}}} ^{{n}} \:\left(\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right){arctanx}\:{dx} \\ $$$$\left.\mathrm{1}\right)\:{calculate}\:{A}_{{n}} \\ $$$$\left.\mathrm{2}\right)\:{find}\:{lim}_{{n}\rightarrow+\infty} \:{A}_{{n}} \\ $$

Question Number 35048 Answers: 0 Comments: 0

find ∫ (dx/(cos(sinx)))

$${find}\:\int\:\:\:\:\:\frac{{dx}}{{cos}\left({sinx}\right)} \\ $$

Question Number 35046 Answers: 0 Comments: 0

find F(x)= ∫_0 ^π ln( 1+x sin^2 t)dt with ∣x∣<1 2) calculate ∫_0 ^π ln(1+(1/2)sin^2 t)dt

$${find}\:{F}\left({x}\right)=\:\int_{\mathrm{0}} ^{\pi} \:{ln}\left(\:\mathrm{1}+{x}\:{sin}^{\mathrm{2}} {t}\right){dt}\:{with}\:\mid{x}\mid<\mathrm{1} \\ $$$$\left.\mathrm{2}\right)\:{calculate}\:\int_{\mathrm{0}} ^{\pi} \:\:{ln}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}{sin}^{\mathrm{2}} {t}\right){dt} \\ $$

Question Number 35045 Answers: 0 Comments: 0

find f(x)=∫_0 ^∞ ((arctan(xt))/(1+t^2 ))dt .

$${find}\:{f}\left({x}\right)=\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{arctan}\left({xt}\right)}{\mathrm{1}+{t}^{\mathrm{2}} }{dt}\:\:. \\ $$

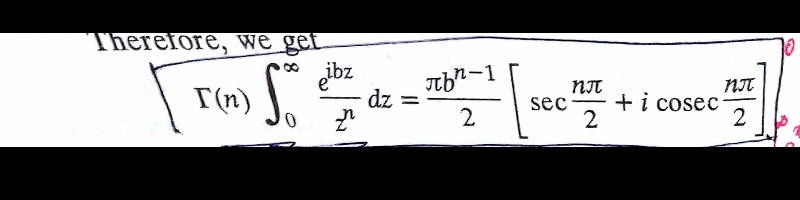
Question Number 35044 Answers: 1 Comments: 1

1)find ∫ (√(1+t^2 )) dt 2) calculate ∫_1 ^(√3) (√(1+t^2 )) dt

$$\left.\mathrm{1}\right){find}\:\int\:\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }\:{dt} \\ $$$$\left.\mathrm{2}\right)\:{calculate}\:\:\int_{\mathrm{1}} ^{\sqrt{\mathrm{3}}} \:\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }\:\:{dt} \\ $$

Question Number 35043 Answers: 1 Comments: 0

let t>0 and F(t) =∫_0 ^∞ ((sin(x^2 ) e^(−tx^2 ) )/x^2 )dx calculate (dF/dt)(t).

$${let}\:{t}>\mathrm{0}\:{and}\:{F}\left({t}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{sin}\left({x}^{\mathrm{2}} \right)\:{e}^{−{tx}^{\mathrm{2}} } }{{x}^{\mathrm{2}} }{dx} \\ $$$${calculate}\:\frac{{dF}}{{dt}}\left({t}\right). \\ $$

Question Number 35041 Answers: 0 Comments: 1

find the value of Σ_(n=1) ^∞ ((n+1)/(n^3 (n+1)^2 ))

$${find}\:{the}\:{value}\:{of}\:\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{{n}+\mathrm{1}}{{n}^{\mathrm{3}} \left({n}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$

Question Number 35040 Answers: 0 Comments: 0

find the value of Σ_(n=1) ^∞ (x^n /(n(n+1)(2n−1))) 2) find the value of Σ_(n=1) ^∞ (((−1)^n )/(2^n n(n+1)(2n−1)))

$${find}\:{the}\:{value}\:{of}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\:\:\:\frac{{x}^{{n}} }{{n}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}−\mathrm{1}\right)} \\ $$$$\left.\mathrm{2}\right)\:{find}\:{the}\:{value}\:{of}\:\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}^{{n}} {n}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}−\mathrm{1}\right)} \\ $$

Question Number 35023 Answers: 1 Comments: 1

Question Number 35021 Answers: 0 Comments: 1

Find the points at which the given function is discontinuous : f(x)= ∣x∣ sgn (x^3 −x) .

$${Find}\:{the}\:{points}\:{at}\:{which}\:{the}\:{given} \\ $$$${function}\:{is}\:{discontinuous}\:: \\ $$$${f}\left({x}\right)=\:\mid{x}\mid\:{sgn}\:\left({x}^{\mathrm{3}} −{x}\right)\:. \\ $$

Question Number 35018 Answers: 1 Comments: 0

∫∫∫((dxdydz)/((x+y+z+1)^3 )) bounded by the coordinate planes and the plane x+y+z=1 .

$$\int\int\int\frac{{dxdydz}}{\left({x}+{y}+{z}+\mathrm{1}\right)^{\mathrm{3}} }\:\:\:{bounded}\:{by}\:{the} \\ $$$${coordinate}\:{planes}\:{and}\:{the}\:{plane} \\ $$$${x}+{y}+{z}=\mathrm{1}\:. \\ $$

Question Number 35015 Answers: 2 Comments: 0

∫(x^2 /((1+x^3 )^2 ))dx

$$\int\frac{{x}^{\mathrm{2}} }{\left(\mathrm{1}+{x}^{\mathrm{3}} \right)^{\mathrm{2}} }{dx} \\ $$

Question Number 35005 Answers: 2 Comments: 0

Find remainder when 1!+2!+3!+...+99!+100! is divided by 12.

$$\mathrm{Find}\:\mathrm{remainder}\:\mathrm{when} \\ $$$$\:\:\:\:\mathrm{1}!+\mathrm{2}!+\mathrm{3}!+...+\mathrm{99}!+\mathrm{100}! \\ $$$$\mathrm{is}\:\mathrm{divided}\:\mathrm{by}\:\:\mathrm{12}. \\ $$

Question Number 35004 Answers: 3 Comments: 0

Prove that 41 divides 2^(20) −1

$$\mathrm{Prove}\:\mathrm{that}\:\mathrm{41}\:\mathrm{divides}\:\mathrm{2}^{\mathrm{20}} −\mathrm{1} \\ $$

Pg 1731 Pg 1732 Pg 1733 Pg 1734 Pg 1735 Pg 1736 Pg 1737 Pg 1738 Pg 1739 Pg 1740

Contact: info@tinkutara.com