
AllQuestion and Answers: Page 1732
Question Number 35909 Answers: 1 Comments: 4
Question Number 35899 Answers: 0 Comments: 2
Question Number 35897 Answers: 0 Comments: 2
$${log}_{{x}^{\mathrm{1}/\mathrm{2}\:} } \mathrm{64}=\mathrm{3}.\:{What}\:{is}\:{x}? \\ $$
Question Number 35895 Answers: 2 Comments: 1

Question Number 35892 Answers: 2 Comments: 2
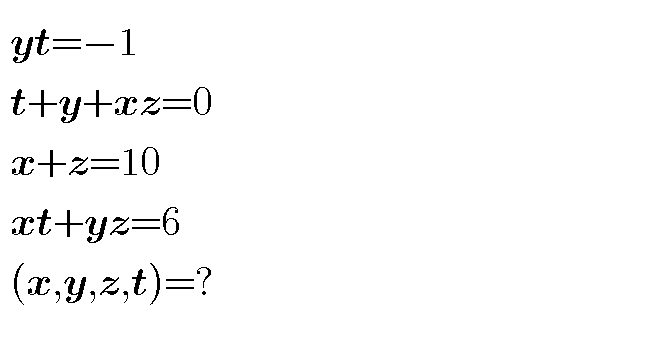
Question Number 35886 Answers: 1 Comments: 0

Question Number 35882 Answers: 0 Comments: 4
Question Number 35881 Answers: 1 Comments: 1
Question Number 35880 Answers: 0 Comments: 0
Question Number 35879 Answers: 1 Comments: 0
Question Number 35878 Answers: 1 Comments: 1
Question Number 35877 Answers: 1 Comments: 0
Question Number 35876 Answers: 0 Comments: 3
Question Number 35873 Answers: 1 Comments: 0
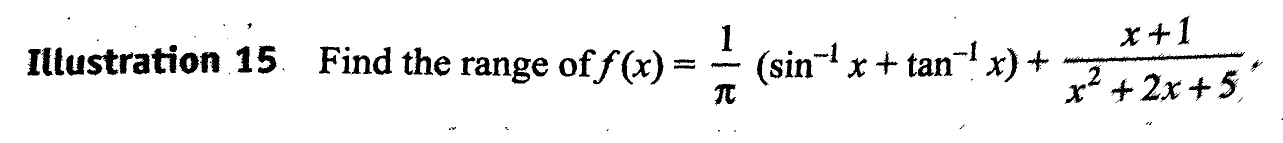
Question Number 35872 Answers: 1 Comments: 1

Question Number 35871 Answers: 0 Comments: 0
Question Number 35848 Answers: 0 Comments: 1
Question Number 35844 Answers: 3 Comments: 1
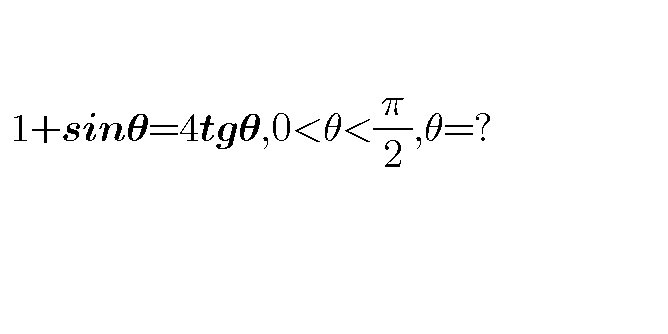
Question Number 35832 Answers: 1 Comments: 3
Question Number 35828 Answers: 1 Comments: 2
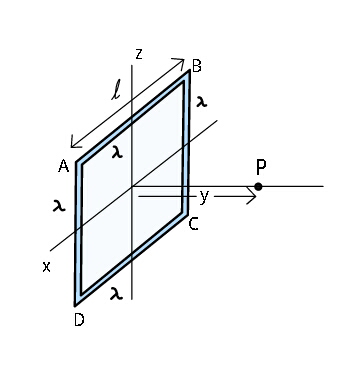
Question Number 35821 Answers: 0 Comments: 4
Question Number 35811 Answers: 3 Comments: 6
Question Number 35798 Answers: 0 Comments: 3

Question Number 35789 Answers: 0 Comments: 1
Question Number 35791 Answers: 1 Comments: 0
Question Number 35771 Answers: 0 Comments: 2

Pg 1727 Pg 1728 Pg 1729 Pg 1730 Pg 1731 Pg 1732 Pg 1733 Pg 1734 Pg 1735 Pg 1736
