Question and Answers Forum

AllQuestion and Answers: Page 1724

Question Number 36711 Answers: 0 Comments: 0

The first term in an AP is the 3rd term in A GP , the 5th term is 30 for the AP, and the 12th term of the GP is 64,find the sum to infinity.

$$\:\:{The}\:\:{first}\:{term}\:{in}\:{an}\:{AP}\:{is}\:{the}\: \\ $$$$\mathrm{3}{rd}\:{term}\:{in}\:{A}\:{GP}\:,\:{the}\:\mathrm{5}{th}\:{term}\:{is} \\ $$$$\mathrm{30}\:{for}\:{the}\:{AP},\:{and}\:{the}\:\mathrm{12}{th}\:{term} \\ $$$${of}\:{the}\:{GP}\:{is}\:\mathrm{64},{find}\:{the}\:{sum}\:{to} \\ $$$${infinity}. \\ $$

Question Number 36714 Answers: 0 Comments: 0

Given the matrix (((3c+1 5 )),((c c)) ) is singular find the value of c and find x if y = mx + c are all natural numbers

$${Given}\:{the}\:{matrix} \\ $$$$\begin{pmatrix}{\mathrm{3}{c}+\mathrm{1}\:\:\:\:\:\:\:\:\mathrm{5}\:}\\{{c}\:\:\:\:\:\:\:\:\:\:\:\:\:\:{c}}\end{pmatrix}\:{is}\:{singular}\: \\ $$$${find}\:{the}\:{value}\:{of}\:{c}\:{and}\: \\ $$$${find}\:{x}\:{if}\:{y}\:=\:{mx}\:+\:{c}\:{are}\:{all} \\ $$$${natural}\:{numbers} \\ $$$$ \\ $$

Question Number 36707 Answers: 2 Comments: 1

P=i^2 R then how (dP/P) = 2 (dI/I) ? Similarly P= (V^2 /R) then how (dP/P)=2(dV/V)?

$$\mathrm{P}=\mathrm{i}^{\mathrm{2}} \mathrm{R}\:\mathrm{then}\:\mathrm{how}\:\frac{\mathrm{dP}}{\mathrm{P}}\:=\:\mathrm{2}\:\frac{\mathrm{dI}}{\mathrm{I}}\:? \\ $$$$\mathrm{Similarly}\:\mathrm{P}=\:\frac{\mathrm{V}^{\mathrm{2}} }{\mathrm{R}}\:\mathrm{then}\:\mathrm{how}\:\frac{\mathrm{dP}}{\mathrm{P}}=\mathrm{2}\frac{\mathrm{dV}}{\mathrm{V}}? \\ $$

Question Number 36703 Answers: 2 Comments: 2

show that f(x)=sin X is derivable at every aεR

$${show}\:{that}\:{f}\left({x}\right)=\mathrm{sin}\:{X}\:{is}\:{derivable}\:{at}\:{every}\:{a}\varepsilon{R} \\ $$

Question Number 36700 Answers: 2 Comments: 0

Question Number 36699 Answers: 0 Comments: 0

Question Number 36696 Answers: 0 Comments: 0

if y=tan^(−1) x show that (1+x^2 )y_(n+2) +2(n+1)xy_(n+1) +n(n+1)y_n =0

$${if}\:{y}={tan}^{−\mathrm{1}} {x}\:{show}\:{that} \\ $$$$\left(\mathrm{1}+{x}^{\mathrm{2}} \right){y}_{{n}+\mathrm{2}} +\mathrm{2}\left({n}+\mathrm{1}\right){xy}_{{n}+\mathrm{1}} +{n}\left({n}+\mathrm{1}\right){y}_{{n}} =\mathrm{0} \\ $$

Question Number 36692 Answers: 2 Comments: 1

x^3 +y^3 =5 x^2 +y^2 =3

$${x}^{\mathrm{3}} +{y}^{\mathrm{3}} =\mathrm{5} \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{3} \\ $$

Question Number 36691 Answers: 0 Comments: 2

Question Number 36689 Answers: 0 Comments: 1

1) find the value of ∫_0 ^1 ln(1−x^3 )dx then find the value of ∫_0 ^1 ln(1+x+x^2 )dx 2)find the value of ∫_0 ^1 ln(1+x^3 )dx then calculate ∫_0 ^1 ln(1−x +x^2 )dx

$$\left.\mathrm{1}\right)\:{find}\:{the}\:{value}\:{of}\:\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}−{x}^{\mathrm{3}} \right){dx}\:{then} \\ $$$${find}\:{the}\:{value}\:{of}\:\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}+{x}+{x}^{\mathrm{2}} \right){dx} \\ $$$$\left.\mathrm{2}\right){find}\:{the}\:{value}\:{of}\:\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}+{x}^{\mathrm{3}} \right){dx}\:{then}\: \\ $$$${calculate}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{ln}\left(\mathrm{1}−{x}\:+{x}^{\mathrm{2}} \right){dx} \\ $$

Question Number 36690 Answers: 0 Comments: 1

let f(t) =∫_0 ^1 ln(1 −tx^3 )dx with 0<t≤1 find a simple form of f(t) 2)calculate ∫_0 ^1 ln(2−x^3 )dx .

$${let}\:\:{f}\left({t}\right)\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:{ln}\left(\mathrm{1}\:−{tx}^{\mathrm{3}} \right){dx}\:\:{with}\:\mathrm{0}<{t}\leqslant\mathrm{1} \\ $$$${find}\:{a}\:{simple}\:{form}\:{of}\:{f}\left({t}\right)\: \\ $$$$\left.\mathrm{2}\right){calculate}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{ln}\left(\mathrm{2}−{x}^{\mathrm{3}} \right){dx}\:. \\ $$

Question Number 36677 Answers: 4 Comments: 3

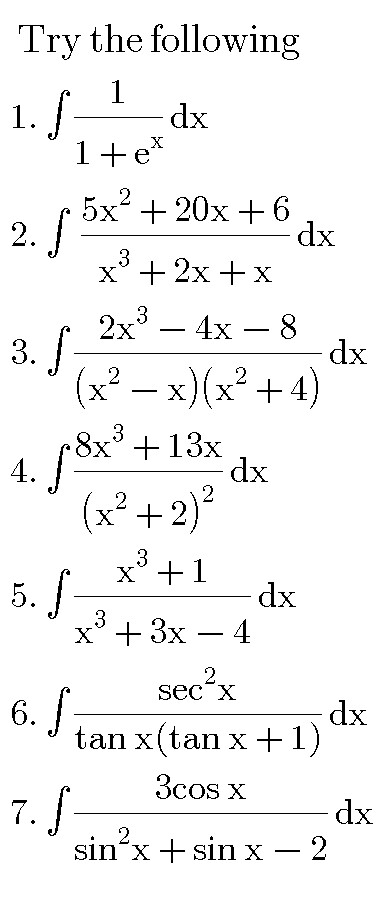
Question Number 36676 Answers: 1 Comments: 3

if z = − 27, find all the root of z in complex plain

$$\mathrm{if}\:\:\mathrm{z}\:=\:−\:\mathrm{27},\:\:\mathrm{find}\:\mathrm{all}\:\mathrm{the}\:\mathrm{root}\:\mathrm{of}\:\mathrm{z}\:\mathrm{in}\:\mathrm{complex}\:\mathrm{plain} \\ $$

Question Number 36661 Answers: 0 Comments: 2

Question Number 36660 Answers: 1 Comments: 0

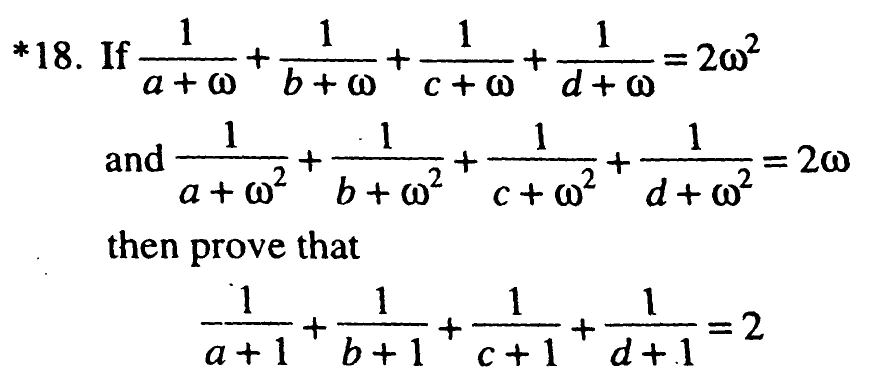
Question Number 36649 Answers: 1 Comments: 4

∫ (1/(x^4 +1)) dx

$$\int\:\frac{\mathrm{1}}{{x}^{\mathrm{4}} +\mathrm{1}}\:{dx} \\ $$

Question Number 36643 Answers: 2 Comments: 1

∫ (x/(x^4 +x^2 +1)) dx = ?

$$\int\:\frac{{x}}{{x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}}\:{dx}\:=\:? \\ $$

Question Number 36634 Answers: 0 Comments: 5

Question Number 36633 Answers: 0 Comments: 1

calculate ∫_0 ^1 arctan(x^2 +x+1)dx

$${calculate}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{arctan}\left({x}^{\mathrm{2}} \:+{x}+\mathrm{1}\right){dx} \\ $$

Question Number 36630 Answers: 0 Comments: 1

Question Number 36629 Answers: 0 Comments: 0

Question Number 36626 Answers: 0 Comments: 1

Question Number 36625 Answers: 0 Comments: 0

Question Number 36623 Answers: 0 Comments: 0

Question Number 36622 Answers: 0 Comments: 0

Question Number 36613 Answers: 1 Comments: 5

Pg 1719 Pg 1720 Pg 1721 Pg 1722 Pg 1723 Pg 1724 Pg 1725 Pg 1726 Pg 1727 Pg 1728

Contact: [email protected]