Question and Answers Forum

AllQuestion and Answers: Page 172

Question Number 202383 Answers: 2 Comments: 0

Show that ((a(√b) − b(√a))/(a(√b) + b(√a))) = (1/(a − b))(a + b − 2(√(ab))).

$$\mathrm{Show}\:\mathrm{that}\:\frac{{a}\sqrt{{b}}\:−\:{b}\sqrt{{a}}}{{a}\sqrt{{b}}\:+\:{b}\sqrt{{a}}}\:=\:\frac{\mathrm{1}}{{a}\:−\:{b}}\left({a}\:+\:{b}\:−\:\mathrm{2}\sqrt{{ab}}\right). \\ $$

Question Number 202376 Answers: 0 Comments: 1

Question Number 202374 Answers: 1 Comments: 2

Question Number 202371 Answers: 2 Comments: 0

If A ∈ M_(2×2) , det(A )≠ 0 , A^( 3) = A^2 +A ⇒ Find the values of det (2A −I )

$$ \\ $$$$\:\:\:{If}\:\:\:\:{A}\:\in\:{M}_{\mathrm{2}×\mathrm{2}} \:,\:{det}\left({A}\:\right)\neq\:\mathrm{0} \\ $$$$\:\:\:\:,\:\:{A}^{\:\mathrm{3}} \:=\:{A}^{\mathrm{2}} \:+{A}\:\Rightarrow\:{Find}\:{the}\: \\ $$$$\:\:\:\:{values}\:{of}\:\:\:{det}\:\left(\mathrm{2}{A}\:−{I}\:\right) \\ $$$$ \\ $$

Question Number 202359 Answers: 1 Comments: 0

2 , 8 , 32 , ... geometfic serie for b_m > 1024 find min(m) = ?

$$\mathrm{2}\:,\:\mathrm{8}\:,\:\mathrm{32}\:,\:...\:\mathrm{geometfic}\:\mathrm{serie} \\ $$$$\mathrm{for}\:\:\:\mathrm{b}_{\boldsymbol{\mathrm{m}}} \:>\:\mathrm{1024}\:\:\:\mathrm{find}\:\:\:\mathrm{min}\left(\mathrm{m}\right)\:=\:? \\ $$

Question Number 202356 Answers: 4 Comments: 0

Find: 1−(sin30°)^2 + (sin30°)^4 − (sin30°)^6 + ...

$$\mathrm{Find}: \\ $$$$\mathrm{1}−\left(\mathrm{sin30}°\right)^{\mathrm{2}} \:+\:\left(\mathrm{sin30}°\right)^{\mathrm{4}} \:−\:\left(\mathrm{sin30}°\right)^{\mathrm{6}} \:+\:... \\ $$

Question Number 202353 Answers: 2 Comments: 0

If 2x = a + (√((4b^3 − a^3 )/(3a))) and 2y = a − (√((4b^3 − a^3 )/(3a))) then show that x^3 + y^3 = b^3 .

$$\mathrm{If}\:\mathrm{2}{x}\:=\:{a}\:+\:\sqrt{\frac{\mathrm{4}{b}^{\mathrm{3}} \:−\:{a}^{\mathrm{3}} }{\mathrm{3}{a}}}\:\mathrm{and} \\ $$$$\mathrm{2}{y}\:=\:{a}\:−\:\sqrt{\frac{\mathrm{4}{b}^{\mathrm{3}} \:−\:{a}^{\mathrm{3}} }{\mathrm{3}{a}}}\:\mathrm{then}\:\mathrm{show}\:\mathrm{that} \\ $$$${x}^{\mathrm{3}} \:+\:{y}^{\mathrm{3}} \:=\:{b}^{\mathrm{3}} \:. \\ $$

Question Number 202352 Answers: 0 Comments: 9

Question Number 202348 Answers: 1 Comments: 0

Let a,b,c ∈R^+ , a+b+c=3 prove the following inequality (((2a−3)^2 )/b)+(((2b−3)^2 )/c)+(((2c−3)^2 )/a)≥((a^2 +b^2 )/(a+b))+((b^2 +c^2 )/(b+c))+((c^2 +a^2 )/(c+a))

$$ \\ $$$$\mathrm{Let}\:{a},{b},{c}\:\:\in\mathbb{R}^{+} \:,\:{a}+{b}+{c}=\mathrm{3}\:\mathrm{prove}\:\mathrm{the}\:\mathrm{following}\:\mathrm{inequality} \\ $$$$\frac{\left(\mathrm{2}{a}−\mathrm{3}\right)^{\mathrm{2}} }{{b}}+\frac{\left(\mathrm{2}{b}−\mathrm{3}\right)^{\mathrm{2}} }{{c}}+\frac{\left(\mathrm{2}{c}−\mathrm{3}\right)^{\mathrm{2}} }{{a}}\geqslant\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }{{a}+{b}}+\frac{{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }{{b}+{c}}+\frac{{c}^{\mathrm{2}} +{a}^{\mathrm{2}} }{{c}+{a}} \\ $$

Question Number 202340 Answers: 2 Comments: 0

Question Number 202329 Answers: 0 Comments: 0

Question Number 202328 Answers: 1 Comments: 1

If n ≥ 2 and U_n = (3 + (√5))^n + (3 − (√5))^n then prove that U_(n + 1) = 6U_n − 4U_(n − 1) .

$$\mathrm{If}\:{n}\:\geqslant\:\mathrm{2}\:\mathrm{and}\:\mathrm{U}_{{n}} \:=\:\left(\mathrm{3}\:+\:\sqrt{\mathrm{5}}\right)^{{n}} \:+\:\left(\mathrm{3}\:−\:\sqrt{\mathrm{5}}\right)^{{n}} \\ $$$$\mathrm{then}\:\mathrm{prove}\:\mathrm{that}\:\mathrm{U}_{{n}\:+\:\mathrm{1}} \:=\:\mathrm{6U}_{{n}} \:−\:\mathrm{4U}_{{n}\:−\:\mathrm{1}} \:. \\ $$

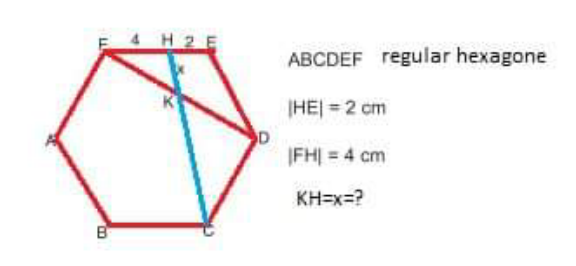
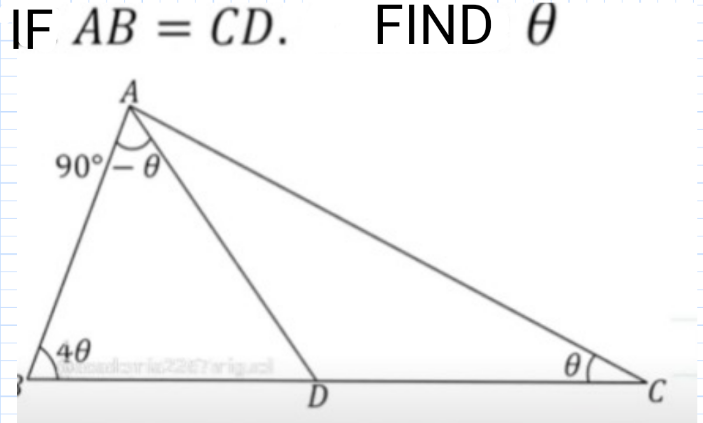
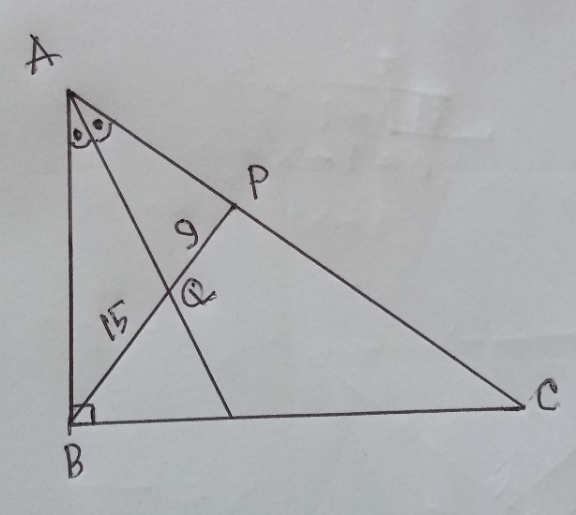
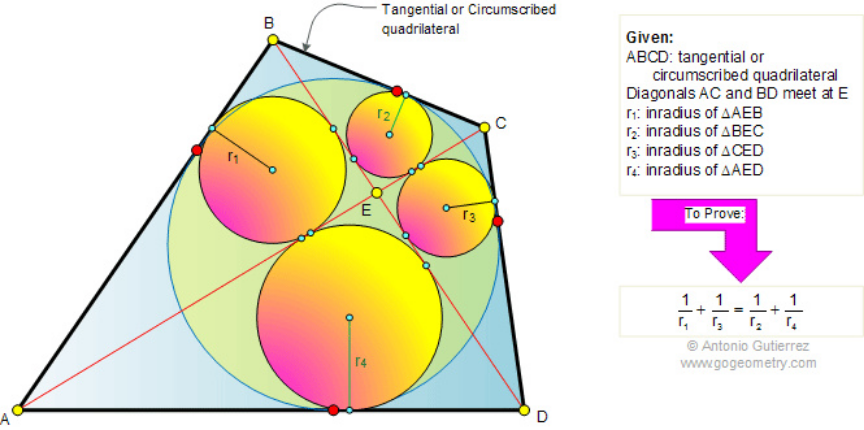
Question Number 202326 Answers: 0 Comments: 0

Question Number 202325 Answers: 1 Comments: 0

Question Number 202324 Answers: 2 Comments: 0

Find: (((1/2) + 1 + (3/2) + ... + 16)/((1/4) + (2/4) + (3/4) + ... + 8))

$$\mathrm{Find}:\:\:\:\frac{\frac{\mathrm{1}}{\mathrm{2}}\:+\:\mathrm{1}\:+\:\frac{\mathrm{3}}{\mathrm{2}}\:+\:...\:+\:\mathrm{16}}{\frac{\mathrm{1}}{\mathrm{4}}\:+\:\frac{\mathrm{2}}{\mathrm{4}}\:+\:\frac{\mathrm{3}}{\mathrm{4}}\:+\:...\:+\:\mathrm{8}} \\ $$

Question Number 202319 Answers: 0 Comments: 0

Question Number 202315 Answers: 1 Comments: 0

If x : y : z = a : b : c then show that (((a + b + c)/(x + y + z)))^3 = ((abc)/(xyz)) .

$$\mathrm{If}\:{x}\::\:{y}\::\:{z}\:=\:{a}\::\:{b}\::\:{c}\:\mathrm{then}\:\mathrm{show}\:\mathrm{that} \\ $$$$\left(\frac{{a}\:+\:{b}\:+\:{c}}{{x}\:+\:{y}\:+\:{z}}\right)^{\mathrm{3}} \:=\:\frac{{abc}}{{xyz}}\:. \\ $$

Question Number 202308 Answers: 0 Comments: 1

Question Number 202307 Answers: 3 Comments: 0

Show that ((a^3 + b^3 )/(a^2 + b^2 )) > ((a^2 + b^2 )/(a + b))

$$\mathrm{Show}\:\mathrm{that}\:\frac{{a}^{\mathrm{3}} \:+\:{b}^{\mathrm{3}} }{{a}^{\mathrm{2}} \:+\:{b}^{\mathrm{2}} }\:>\:\frac{{a}^{\mathrm{2}} \:+\:{b}^{\mathrm{2}} }{{a}\:+\:{b}} \\ $$

Question Number 202306 Answers: 2 Comments: 0

Find the 2023rd term in the sequence 2,3,5,6,7,8,10,11,12,13,14,15,17,18,... obtained by subtracting integer squares from natural numbers.

$$ \\ $$Find the 2023rd term in the sequence 2,3,5,6,7,8,10,11,12,13,14,15,17,18,... obtained by subtracting integer squares from natural numbers.

Question Number 202303 Answers: 3 Comments: 0

If a_1 = 1 and a_1 ∙ a_2 ∙ ... ∙ a_n = n^2 Find: a_2 + a_(13) = ?

$$\mathrm{If}\:\:\:\mathrm{a}_{\mathrm{1}} \:=\:\mathrm{1}\:\:\:\mathrm{and}\:\:\:\mathrm{a}_{\mathrm{1}} \:\centerdot\:\mathrm{a}_{\mathrm{2}} \:\centerdot\:...\:\centerdot\:\mathrm{a}_{\boldsymbol{\mathrm{n}}} \:=\:\mathrm{n}^{\mathrm{2}} \\ $$$$\mathrm{Find}:\:\:\:\mathrm{a}_{\mathrm{2}} \:+\:\mathrm{a}_{\mathrm{13}} \:=\:? \\ $$

Question Number 202302 Answers: 2 Comments: 0

If ((3cosx + 2sinx)/(cosx − sinx)) = 4 find ctgx = ?

$$\mathrm{If}\:\:\:\frac{\mathrm{3cosx}\:+\:\mathrm{2sinx}}{\mathrm{cosx}\:−\:\mathrm{sinx}}\:=\:\mathrm{4}\:\:\:\mathrm{find}\:\:\:\mathrm{ctgx}\:=\:? \\ $$

Question Number 202300 Answers: 1 Comments: 0

Parvin leaves home to go to school. After walking 3/8 of the way, he remembers that he forgot his book. He goes back home, picks up his book, and arrives at school at the time he was originally supposed to. How many times did Parvin increase his initial speed to reach school on time ?

$$ \\ $$Parvin leaves home to go to school. After walking 3/8 of the way, he remembers that he forgot his book. He goes back home, picks up his book, and arrives at school at the time he was originally supposed to. How many times did Parvin increase his initial speed to reach school on time ?

Question Number 202298 Answers: 1 Comments: 0

x ∈ R Find: max((5/(x^2 − 6x + 11))) = ?

$$\mathrm{x}\:\in\:\mathbb{R} \\ $$$$\mathrm{Find}:\:\:\:\boldsymbol{\mathrm{max}}\left(\frac{\mathrm{5}}{\mathrm{x}^{\mathrm{2}} \:−\:\mathrm{6x}\:+\:\mathrm{11}}\right)\:=\:? \\ $$

Question Number 202297 Answers: 2 Comments: 0

If a^2 + a = 5 Find ((a^(−b) + a^(1−b) + a^(2−b) )/a^(−b) ) = ?

$$\mathrm{If}\:\:\:\mathrm{a}^{\mathrm{2}} \:+\:\mathrm{a}\:=\:\mathrm{5} \\ $$$$\mathrm{Find}\:\:\:\frac{\mathrm{a}^{−\boldsymbol{\mathrm{b}}} \:+\:\mathrm{a}^{\mathrm{1}−\boldsymbol{\mathrm{b}}} \:+\:\mathrm{a}^{\mathrm{2}−\boldsymbol{\mathrm{b}}} }{\mathrm{a}^{−\boldsymbol{\mathrm{b}}} }\:=\:? \\ $$

Question Number 202296 Answers: 1 Comments: 0

Find: log_2 (log_3 (log_4 64)) = ?

$$\mathrm{Find}: \\ $$$$\mathrm{log}_{\mathrm{2}} \:\left(\mathrm{log}_{\mathrm{3}} \:\left(\mathrm{log}_{\mathrm{4}} \:\mathrm{64}\right)\right)\:=\:? \\ $$

Pg 167 Pg 168 Pg 169 Pg 170 Pg 171 Pg 172 Pg 173 Pg 174 Pg 175 Pg 176

Contact: info@tinkutara.com