
AllQuestion and Answers: Page 1709
Question Number 38108 Answers: 0 Comments: 1
Question Number 38107 Answers: 0 Comments: 0
Question Number 38106 Answers: 0 Comments: 1
Question Number 38105 Answers: 1 Comments: 0
Question Number 38104 Answers: 1 Comments: 0
Question Number 38103 Answers: 0 Comments: 0
Question Number 38102 Answers: 0 Comments: 0
Question Number 38101 Answers: 0 Comments: 1
Question Number 38100 Answers: 0 Comments: 1
Question Number 38099 Answers: 0 Comments: 5
$${x}^{{x}} =\mathrm{0}.\mathrm{25} \\ $$$${find}\:{x} \\ $$
Question Number 38094 Answers: 1 Comments: 12

Question Number 38092 Answers: 0 Comments: 5

Question Number 38079 Answers: 1 Comments: 4

Question Number 38074 Answers: 1 Comments: 4
$$\int\frac{{dx}}{{a}+{b}\mathrm{tan}\:^{\mathrm{2}} {x}}\:=\:? \\ $$
Question Number 38062 Answers: 0 Comments: 3

Question Number 38059 Answers: 1 Comments: 0
$${Prove}\:{that}\:\Sigma\left({x}_{{i}} −\overset{−} {{x}}\right)=\mathrm{0} \\ $$
Question Number 38058 Answers: 3 Comments: 0
$$\int\frac{\mathrm{tan}\:{x}}{{a}+{b}\mathrm{tan}\:^{\mathrm{2}} {x}}\:{dx}\:\:=\:? \\ $$
Question Number 38057 Answers: 1 Comments: 0
Question Number 38051 Answers: 0 Comments: 0
Question Number 38049 Answers: 1 Comments: 0
Question Number 38044 Answers: 2 Comments: 1

Question Number 38032 Answers: 1 Comments: 1
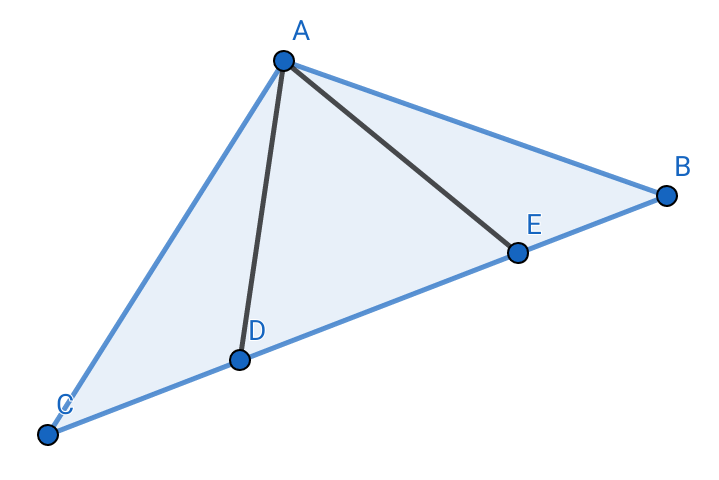
Question Number 38025 Answers: 1 Comments: 0
Question Number 38024 Answers: 1 Comments: 0

Question Number 38015 Answers: 0 Comments: 6
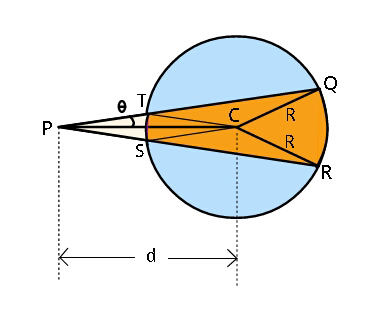
Question Number 38012 Answers: 3 Comments: 1
Pg 1704 Pg 1705 Pg 1706 Pg 1707 Pg 1708 Pg 1709 Pg 1710 Pg 1711 Pg 1712 Pg 1713
