
AllQuestion and Answers: Page 1707
Question Number 38284 Answers: 1 Comments: 2
Question Number 38282 Answers: 1 Comments: 0

Question Number 38281 Answers: 1 Comments: 0

Question Number 38262 Answers: 1 Comments: 0

Question Number 38252 Answers: 0 Comments: 2
Question Number 38250 Answers: 0 Comments: 0
Question Number 38247 Answers: 2 Comments: 2
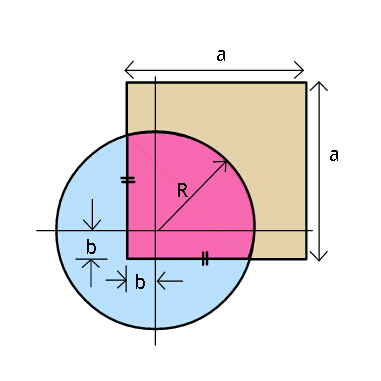
Question Number 38235 Answers: 0 Comments: 4
Question Number 38261 Answers: 1 Comments: 0

Question Number 38232 Answers: 4 Comments: 1
Question Number 38222 Answers: 0 Comments: 1
Question Number 38211 Answers: 0 Comments: 2
Question Number 38210 Answers: 2 Comments: 4
Question Number 38209 Answers: 0 Comments: 2
Question Number 38208 Answers: 0 Comments: 3
Question Number 38207 Answers: 0 Comments: 1
Question Number 38206 Answers: 1 Comments: 1
Question Number 38205 Answers: 0 Comments: 0
Question Number 38204 Answers: 0 Comments: 1
Question Number 38203 Answers: 0 Comments: 0
Question Number 38202 Answers: 0 Comments: 1
Question Number 38201 Answers: 0 Comments: 0
Question Number 38199 Answers: 1 Comments: 0
Question Number 38198 Answers: 0 Comments: 5
Question Number 38197 Answers: 0 Comments: 1
Question Number 38195 Answers: 0 Comments: 1
Pg 1702 Pg 1703 Pg 1704 Pg 1705 Pg 1706 Pg 1707 Pg 1708 Pg 1709 Pg 1710 Pg 1711
