
AllQuestion and Answers: Page 1704
Question Number 38696 Answers: 1 Comments: 0
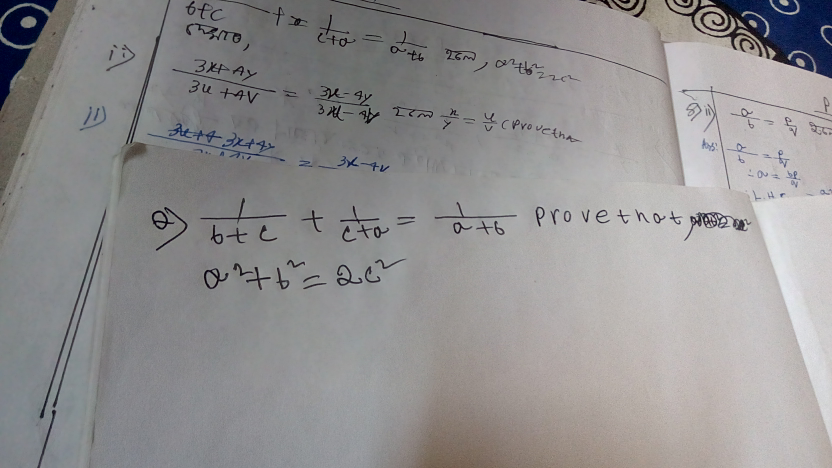
Question Number 38692 Answers: 1 Comments: 0
Question Number 38675 Answers: 1 Comments: 3

Question Number 38679 Answers: 3 Comments: 0

Question Number 38651 Answers: 1 Comments: 0
Question Number 38643 Answers: 1 Comments: 4
Question Number 38642 Answers: 0 Comments: 3
Question Number 38641 Answers: 0 Comments: 1
Question Number 38640 Answers: 0 Comments: 1
$${calculate}\:\sum_{{k}=\mathrm{1}} ^{{n}} {k}^{\mathrm{4}} \:\:{interms}\:{of}\:{n}. \\ $$
Question Number 38636 Answers: 1 Comments: 0
Question Number 38618 Answers: 1 Comments: 2

Question Number 38613 Answers: 1 Comments: 0
Question Number 39491 Answers: 0 Comments: 0

Question Number 38600 Answers: 3 Comments: 1

Question Number 38593 Answers: 1 Comments: 3

Question Number 38587 Answers: 2 Comments: 2
Question Number 38570 Answers: 0 Comments: 2

Question Number 38568 Answers: 0 Comments: 18
Question Number 38562 Answers: 1 Comments: 0
$$\left(\sqrt{\mathrm{2}}\:+{i}\right)\left(\mathrm{1}−\sqrt{\mathrm{2}{i}}\:\right) \\ $$
Question Number 38559 Answers: 1 Comments: 0
Question Number 38557 Answers: 1 Comments: 0
Question Number 38536 Answers: 2 Comments: 0
$$\int_{\mathrm{0}} ^{\pi} \frac{{dx}}{\sqrt{\mathrm{3}−\mathrm{cos}\:{x}}}= \\ $$
Question Number 38535 Answers: 0 Comments: 0
Question Number 38534 Answers: 0 Comments: 0
$$\int\underset{{R}} {\int}\left(\mathrm{2}{x}\:+\:\mathrm{3}{y}\right)^{\mathrm{2}} \:{dA}=?? \\ $$
Question Number 38533 Answers: 2 Comments: 2

Question Number 38521 Answers: 0 Comments: 1
Pg 1699 Pg 1700 Pg 1701 Pg 1702 Pg 1703 Pg 1704 Pg 1705 Pg 1706 Pg 1707 Pg 1708
