Question and Answers Forum

AllQuestion and Answers: Page 1703

Question Number 37309 Answers: 1 Comments: 2

calculate ∫_0 ^(+∞) (x^2 /((1+x^2 )^3 )) dx .

$${calculate}\:\:\int_{\mathrm{0}} ^{+\infty} \:\:\:\frac{{x}^{\mathrm{2}} }{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{3}} }\:{dx}\:. \\ $$

Question Number 37307 Answers: 0 Comments: 1

calculate ∫_γ (dz/z) with γ ={z∈C /∣z∣=1} .

$${calculate}\:\:\:\int_{\gamma} \:\:\:\:\frac{{dz}}{{z}}\:\:\:{with}\:\gamma\:=\left\{{z}\in{C}\:/\mid{z}\mid=\mathrm{1}\right\}\:. \\ $$

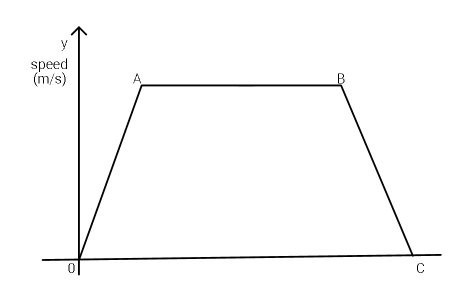
Question Number 37306 Answers: 0 Comments: 1

calculate ∫_(−∞) ^(+∞) e^(ix) ((x−i)/((x+i)(x^2 +3))) dx .

$${calculate}\:\int_{−\infty} ^{+\infty} \:\:\:{e}^{{ix}} \:\:\:\frac{{x}−{i}}{\left({x}+{i}\right)\left({x}^{\mathrm{2}} \:+\mathrm{3}\right)}\:{dx}\:. \\ $$$$ \\ $$

Question Number 37304 Answers: 0 Comments: 1

calculate ∫_(−∞) ^(+∞) ((5+e^(ix) )/((3+e^(ix) )(1+x^2 )))dx .

$${calculate}\:\int_{−\infty} ^{+\infty} \:\:\:\frac{\mathrm{5}+{e}^{{ix}} }{\left(\mathrm{3}+{e}^{{ix}} \right)\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{dx}\:. \\ $$

Question Number 37303 Answers: 0 Comments: 1

calculate ∫_γ (dz/(z^3 +8)) in those cases 1) γ ={z∈C / ∣z∣ =1} 2) γ ={z∈C / ∣z∣ =3}

$${calculate}\:\:\int_{\gamma} \:\:\:\:\:\:\frac{{dz}}{{z}^{\mathrm{3}} \:+\mathrm{8}}\:{in}\:{those}\:{cases} \\ $$$$\left.\mathrm{1}\right)\:\gamma\:=\left\{{z}\in{C}\:/\:\mid{z}\mid\:=\mathrm{1}\right\} \\ $$$$\left.\mathrm{2}\right)\:\gamma\:=\left\{{z}\in{C}\:/\:\mid{z}\mid\:=\mathrm{3}\right\} \\ $$

Question Number 37302 Answers: 0 Comments: 0

let γ = {z∈C / ∣z∣ =4} calculate ∫_γ (dz/(z sinz)) in the positif sens.

$${let}\:\gamma\:=\:\left\{{z}\in{C}\:/\:\mid{z}\mid\:=\mathrm{4}\right\}\: \\ $$$${calculate}\:\:\int_{\gamma} \:\:\:\:\:\frac{{dz}}{{z}\:{sinz}}\:{in}\:{the}\:{positif}\:{sens}. \\ $$

Question Number 37301 Answers: 0 Comments: 0

find?the value of ∫_(−∞) ^(+∞) (((2x+1)e^(−x^2 ) )/(1+4x^2 )) dx .

$${find}?{the}\:{value}\:{of}\:\:\int_{−\infty} ^{+\infty} \:\:\:\frac{\left(\mathrm{2}{x}+\mathrm{1}\right){e}^{−{x}^{\mathrm{2}} } }{\mathrm{1}+\mathrm{4}{x}^{\mathrm{2}} }\:{dx}\:. \\ $$

Question Number 37300 Answers: 0 Comments: 1

let f(z)=(((1−z^2 )e^(2z) )/z^3 ) calculate Res(f, 0)

$${let}\:{f}\left({z}\right)=\frac{\left(\mathrm{1}−{z}^{\mathrm{2}} \right){e}^{\mathrm{2}{z}} }{{z}^{\mathrm{3}} } \\ $$$${calculate}\:{Res}\left({f},\:\mathrm{0}\right) \\ $$

Question Number 37299 Answers: 0 Comments: 1

calculate ∫_C ((9(z^2 +2))/(z(z+1)^3 (z−2)))dz with C is the circle C ={z∈C/ ∣z∣ =3}

$${calculate}\:\:\int_{{C}} \:\:\:\frac{\mathrm{9}\left({z}^{\mathrm{2}} \:+\mathrm{2}\right)}{{z}\left({z}+\mathrm{1}\right)^{\mathrm{3}} \left({z}−\mathrm{2}\right)}{dz}\:\:{with}\:\:{C}\:{is}\:{the} \\ $$$${circle}\:{C}\:=\left\{{z}\in{C}/\:\mid{z}\mid\:=\mathrm{3}\right\}\: \\ $$

Question Number 37298 Answers: 0 Comments: 1

calculate ∫_γ ((z+1)/(z(z−1)(z+2)))dz with γ is the circle γ ={z∈C/ ∣z∣ =(3/2)}

$${calculate}\:\:\int_{\gamma} \:\:\:\:\frac{{z}+\mathrm{1}}{{z}\left({z}−\mathrm{1}\right)\left({z}+\mathrm{2}\right)}{dz}\:\:{with}\:\gamma\:{is}\:{the} \\ $$$${circle}\:\gamma\:=\left\{{z}\in{C}/\:\:\mid{z}\mid\:=\frac{\mathrm{3}}{\mathrm{2}}\right\} \\ $$

Question Number 37297 Answers: 0 Comments: 1

calculate ∫_C (z/(z^2 +1))dz with C={z∈C/∣z∣=(1/2)}

$${calculate}\:\:\int_{{C}} \:\:\:\:\frac{{z}}{{z}^{\mathrm{2}} \:+\mathrm{1}}{dz}\:\:{with}\:{C}=\left\{{z}\in{C}/\mid{z}\mid=\frac{\mathrm{1}}{\mathrm{2}}\right\} \\ $$

Question Number 37296 Answers: 0 Comments: 1

solve sinz =2 zfromC

$${solve}\:{sinz}\:=\mathrm{2}\:\:\:\:\:{zfromC} \\ $$$$ \\ $$

Question Number 37295 Answers: 0 Comments: 0

find the principal value of{(1+i)^(1−i) }^(1+i) .

$${find}\:{the}\:{principal}\:{value}\:{of}\left\{\left(\mathrm{1}+{i}\right)^{\mathrm{1}−{i}} \right\}^{\mathrm{1}+{i}} . \\ $$

Question Number 37294 Answers: 0 Comments: 0

let D =D(0,1) and f(z) =Σ_(n=0) ^∞ a_n z^n is a holomorphe function / ∣f(x)∣< (1/(1−∣z∣)) prove that ∣a_n ∣≤ (n+1)(1+(1/n))^n ≤(n+1)e.

$${let}\:{D}\:={D}\left(\mathrm{0},\mathrm{1}\right)\:{and}\:{f}\left({z}\right)\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:{a}_{{n}} {z}^{{n}} \:{is}\:{a}\:{holomorphe} \\ $$$${function}\:/\:\:\mid{f}\left({x}\right)\mid<\:\:\frac{\mathrm{1}}{\mathrm{1}−\mid{z}\mid}\:\:{prove}\:{that} \\ $$$$\mid{a}_{{n}} \mid\leqslant\:\left({n}+\mathrm{1}\right)\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)^{{n}} \leqslant\left({n}+\mathrm{1}\right){e}. \\ $$

Question Number 37291 Answers: 0 Comments: 1

calculate g(θ) = ∫_(−∞) ^(+∞) e^(−x^2 ) sin(sinθ x^2 )dx .

$${calculate}\:{g}\left(\theta\right)\:=\:\int_{−\infty} ^{+\infty} \:{e}^{−{x}^{\mathrm{2}} } \:{sin}\left({sin}\theta\:{x}^{\mathrm{2}} \right){dx}\:. \\ $$

Question Number 37290 Answers: 0 Comments: 0

find f(θ) = ∫_(−∞) ^(+∞) e^(−x^2 ) cos(cosθx)dx .

$${find}\:\:{f}\left(\theta\right)\:=\:\int_{−\infty} ^{+\infty} \:{e}^{−{x}^{\mathrm{2}} } \:{cos}\left({cos}\theta{x}\right){dx}\:. \\ $$

Question Number 37289 Answers: 0 Comments: 0

calculate ∫_0 ^(2π) (dx/(cos^2 t +4sin^2 t))dt .

$${calculate}\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\:\:\:\:\:\frac{{dx}}{{cos}^{\mathrm{2}} {t}\:\:+\mathrm{4}{sin}^{\mathrm{2}} {t}}{dt}\:. \\ $$

Question Number 37288 Answers: 0 Comments: 1

calculate f(α) = ∫_(−∞) ^(+∞) ((cos(2x))/(1+ax^2 )) dx with a>0 2) find the value of ∫_(−∞) ^(+∞) ((cos(2x))/(1+3x^2 )) dx .

$${calculate}\:\:{f}\left(\alpha\right)\:=\:\int_{−\infty} ^{+\infty} \:\:\:\frac{{cos}\left(\mathrm{2}{x}\right)}{\mathrm{1}+{ax}^{\mathrm{2}} }\:{dx}\:{with}\:{a}>\mathrm{0} \\ $$$$\left.\mathrm{2}\right)\:{find}\:{the}\:{value}\:{of}\:\:\int_{−\infty} ^{+\infty} \:\:\:\:\frac{{cos}\left(\mathrm{2}{x}\right)}{\mathrm{1}+\mathrm{3}{x}^{\mathrm{2}} }\:{dx}\:. \\ $$

Question Number 37287 Answers: 0 Comments: 1

calculate f(t) = ∫_(−∞) ^(+∞) ((cos(tx))/(1+x^2 )) dx

$${calculate}\:\:{f}\left({t}\right)\:=\:\int_{−\infty} ^{+\infty} \:\:\:\frac{{cos}\left({tx}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }\:{dx} \\ $$

Question Number 37285 Answers: 0 Comments: 3

let A_n = ∫_0 ^∞ e^(−nx^2 ) sin((x/n))dx with n integr not 0 1) calculate A_n 2) find lim_(n→+∞) A_n

$${let}\:{A}_{{n}} =\:\int_{\mathrm{0}} ^{\infty} \:\:{e}^{−{nx}^{\mathrm{2}} } {sin}\left(\frac{{x}}{{n}}\right){dx}\:\:{with}\:{n}\:{integr}\:{not}\:\mathrm{0} \\ $$$$\left.\mathrm{1}\right)\:{calculate}\:{A}_{{n}} \\ $$$$\left.\mathrm{2}\right)\:{find}\:{lim}_{{n}\rightarrow+\infty} \:{A}_{{n}} \\ $$

Question Number 37284 Answers: 0 Comments: 1

find A_n = ∫_0 ^1 (x^n /(ch(x))) dx .

$${find}\:\:{A}_{{n}} \:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{x}^{{n}} }{{ch}\left({x}\right)}\:{dx}\:. \\ $$

Question Number 37283 Answers: 0 Comments: 1

find ∫_0 ^∞ ((cosx)/(ch(x))) dx .

$${find}\:\:\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\:\frac{{cosx}}{{ch}\left({x}\right)}\:{dx}\:. \\ $$

Question Number 37282 Answers: 0 Comments: 5

let f(x)=(x/(1+x^2 +x^4 )) 1) find f^((n)) (x) 2)calculate f^((n)) (0) 3)developp f at integr serie.

$${let}\:{f}\left({x}\right)=\frac{{x}}{\mathrm{1}+{x}^{\mathrm{2}} \:+{x}^{\mathrm{4}} } \\ $$$$\left.\mathrm{1}\right)\:{find}\:{f}^{\left({n}\right)} \left({x}\right) \\ $$$$\left.\mathrm{2}\right){calculate}\:{f}^{\left({n}\right)} \left(\mathrm{0}\right) \\ $$$$\left.\mathrm{3}\right){developp}\:{f}\:{at}\:{integr}\:{serie}. \\ $$

Question Number 37281 Answers: 0 Comments: 1

find a better approximation for the integrals 1) ∫_0 ^1 e^(−x^2 ) dx 2) ∫_1 ^(+∞) e^(−x^2 ) dx .

$${find}\:{a}\:{better}\:{approximation}\:{for}\:{the} \\ $$$${integrals}\: \\ $$$$\left.\mathrm{1}\right)\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:{e}^{−{x}^{\mathrm{2}} } {dx} \\ $$$$\left.\mathrm{2}\right)\:\int_{\mathrm{1}} ^{+\infty} \:{e}^{−{x}^{\mathrm{2}} } {dx}\:. \\ $$

Question Number 37280 Answers: 0 Comments: 1

calculate ∫_0 ^6 (e^(x−[x]) /(1+e^x ))dx .

$${calculate}\:\:\int_{\mathrm{0}} ^{\mathrm{6}} \:\:\:\frac{{e}^{{x}−\left[{x}\right]} }{\mathrm{1}+{e}^{{x}} }{dx}\:. \\ $$

Question Number 37279 Answers: 1 Comments: 1

cslculate ∫∫_([0,1]^2 ) (x−y)e^(−x−y) dxdy .

$${cslculate}\:\int\int_{\left[\mathrm{0},\mathrm{1}\right]^{\mathrm{2}} } \:\:\:\left({x}−{y}\right){e}^{−{x}−{y}} {dxdy}\:. \\ $$

Pg 1698 Pg 1699 Pg 1700 Pg 1701 Pg 1702 Pg 1703 Pg 1704 Pg 1705 Pg 1706 Pg 1707

Contact: info@tinkutara.com