Question and Answers Forum

AllQuestion and Answers: Page 1701

Question Number 38232 Answers: 4 Comments: 1

Differentiate tan^(−1) ((((√(1+x^2 ))−1)/x)) without using any trigonometric substitution !

$$\mathrm{Differentiate}\: \\ $$$$\mathrm{tan}^{−\mathrm{1}} \left(\frac{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }−\mathrm{1}}{{x}}\right)\:\: \\ $$$${without}\:{using}\:{any}\:{trigonometric}\: \\ $$$${substitution}\:! \\ $$

Question Number 38222 Answers: 0 Comments: 1

If U={−5, −4, −3, −2, −1, 0, 1, 2, 3, 4, 5} A={x/x^2 =25, x ∈ Z} B={x/x^2 +5=9, x ∈ Z} and C={x/−2≤ x ≤ 2, x ∈ Z} then (A ∩ B ∩ C)^c ∩ (A△B)^c =?

$$\mathrm{If}\:\mathbb{U}=\left\{−\mathrm{5},\:−\mathrm{4},\:−\mathrm{3},\:−\mathrm{2},\:−\mathrm{1},\:\mathrm{0},\:\mathrm{1},\:\mathrm{2},\:\mathrm{3},\:\mathrm{4},\:\mathrm{5}\right\} \\ $$$$\mathrm{A}=\left\{{x}/{x}^{\mathrm{2}} =\mathrm{25},\:{x}\:\in\:\mathrm{Z}\right\} \\ $$$$\mathrm{B}=\left\{{x}/{x}^{\mathrm{2}} +\mathrm{5}=\mathrm{9},\:{x}\:\in\:\mathrm{Z}\right\}\:\mathrm{and} \\ $$$$\mathrm{C}=\left\{{x}/−\mathrm{2}\leqslant\:{x}\:\leqslant\:\mathrm{2},\:{x}\:\in\:\mathrm{Z}\right\}\:\mathrm{then} \\ $$$$\left(\mathrm{A}\:\cap\:\mathrm{B}\:\cap\:\mathrm{C}\right)^{\mathrm{c}} \:\cap\:\left(\mathrm{A}\bigtriangleup\mathrm{B}\right)^{\mathrm{c}} =? \\ $$

Question Number 38211 Answers: 0 Comments: 2

let x>0 and F(x)= ∫_0 ^(+∞) ((arctan(xt^2 ))/(1+t^2 ))dt 1) find a simple form of F(x) 2)find the value of ∫_0 ^∞ ((arctan(2t^2 ))/(1+t^2 ))dt 3)find the value of ∫_0 ^∞ ((arctan(3t^2 ))/(1+t^2 ))dt.

$${let}\:{x}>\mathrm{0}\:{and}\:{F}\left({x}\right)=\:\int_{\mathrm{0}} ^{+\infty} \:\frac{{arctan}\left({xt}^{\mathrm{2}} \right)}{\mathrm{1}+{t}^{\mathrm{2}} }{dt} \\ $$$$\left.\mathrm{1}\right)\:{find}\:{a}\:{simple}\:{form}\:{of}\:{F}\left({x}\right) \\ $$$$\left.\mathrm{2}\right){find}\:{the}\:{value}\:{of}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{arctan}\left(\mathrm{2}{t}^{\mathrm{2}} \right)}{\mathrm{1}+{t}^{\mathrm{2}} }{dt} \\ $$$$\left.\mathrm{3}\right){find}\:{the}\:{value}\:{of}\:\int_{\mathrm{0}} ^{\infty} \frac{{arctan}\left(\mathrm{3}{t}^{\mathrm{2}} \right)}{\mathrm{1}+{t}^{\mathrm{2}} }{dt}. \\ $$

Question Number 38210 Answers: 2 Comments: 4

let f(a)= ∫_0 ^π (dθ/(a +sin^2 θ)) (a from R) 1) find f(a) 2)calculate g(a)= ∫_0 ^π (dθ/((a+sin^2 θ)^2 )) 3)calculate ∫_0 ^π (dθ/(1+sin^2 θ)) and ∫_0 ^π (dθ/(2+sin^2 θ)) 4) calculate ∫_0 ^π (dθ/((3 +sin^2 θ)^2 )) .

$${let}\:{f}\left({a}\right)=\:\int_{\mathrm{0}} ^{\pi} \:\:\:\frac{{d}\theta}{{a}\:+{sin}^{\mathrm{2}} \theta}\:\:\:\left({a}\:{from}\:{R}\right) \\ $$$$\left.\mathrm{1}\right)\:{find}\:{f}\left({a}\right) \\ $$$$\left.\mathrm{2}\right){calculate}\:{g}\left({a}\right)=\:\int_{\mathrm{0}} ^{\pi} \:\:\:\frac{{d}\theta}{\left({a}+{sin}^{\mathrm{2}} \theta\right)^{\mathrm{2}} } \\ $$$$\left.\mathrm{3}\right){calculate}\:\int_{\mathrm{0}} ^{\pi} \:\:\:\:\frac{{d}\theta}{\mathrm{1}+{sin}^{\mathrm{2}} \theta}\:{and}\:\int_{\mathrm{0}} ^{\pi} \:\:\frac{{d}\theta}{\mathrm{2}+{sin}^{\mathrm{2}} \theta} \\ $$$$\left.\mathrm{4}\right)\:{calculate}\:\int_{\mathrm{0}} ^{\pi} \:\:\:\frac{{d}\theta}{\left(\mathrm{3}\:+{sin}^{\mathrm{2}} \theta\right)^{\mathrm{2}} }\:. \\ $$

Question Number 38209 Answers: 0 Comments: 2

let f(x)=e^(−x) cosx developp f at fourier serie 1) find the value of Σ_(n=−∞) ^(+∞) (((−1)^n )/(1+n^2 )) 2) calculate Σ_(n=0) ^∞ (1/(n^2 +1)) .

$${let}\:{f}\left({x}\right)={e}^{−{x}} {cosx} \\ $$$${developp}\:{f}\:{at}\:{fourier}\:{serie} \\ $$$$\left.\mathrm{1}\right)\:{find}\:{the}\:{value}\:{of}\:\sum_{{n}=−\infty} ^{+\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{1}+{n}^{\mathrm{2}} } \\ $$$$\left.\mathrm{2}\right)\:{calculate}\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{1}}{{n}^{\mathrm{2}} \:+\mathrm{1}}\:. \\ $$

Question Number 38208 Answers: 0 Comments: 3

let f(x)=ch(αx) developp f at fourier serie. (f 2π periodic even)

$${let}\:{f}\left({x}\right)={ch}\left(\alpha{x}\right)\: \\ $$$${developp}\:{f}\:{at}\:{fourier}\:{serie}. \\ $$$$\left({f}\:\mathrm{2}\pi\:{periodic}\:{even}\right) \\ $$

Question Number 38207 Answers: 0 Comments: 1

prove that coth(x)−(1/x) =Σ_(n=1) ^∞ ((2x)/(x^2 +n^2 π^2 )) (x≠0)

$${prove}\:{that}\:{coth}\left({x}\right)−\frac{\mathrm{1}}{{x}}\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\mathrm{2}{x}}{{x}^{\mathrm{2}} \:+{n}^{\mathrm{2}} \pi^{\mathrm{2}} } \\ $$$$\left({x}\neq\mathrm{0}\right) \\ $$

Question Number 38206 Answers: 1 Comments: 1

calculate lim_(x→0) ((x coth(x)−1)/x^2 )

$${calculate}\:{lim}_{{x}\rightarrow\mathrm{0}} \:\frac{{x}\:{coth}\left({x}\right)−\mathrm{1}}{{x}^{\mathrm{2}} } \\ $$

Question Number 38205 Answers: 0 Comments: 0

if (1/(sinx)) =Σ_(n=1) ^∞ a_n sin(nx) find the values of a_n .

$${if}\:\:\frac{\mathrm{1}}{{sinx}}\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:{a}_{{n}} {sin}\left({nx}\right)\:\:{find}\:{the}\:{values}\:{of} \\ $$$${a}_{{n}} . \\ $$

Question Number 38204 Answers: 0 Comments: 1

if (1/(cosx)) =(a_0 /2) +Σ_(n=1) ^∞ a_n cos(nx) calculate a_0 and a_n

$${if}\:\:\frac{\mathrm{1}}{{cosx}}\:=\frac{{a}_{\mathrm{0}} }{\mathrm{2}}\:+\sum_{{n}=\mathrm{1}} ^{\infty} \:{a}_{{n}} {cos}\left({nx}\right) \\ $$$${calculate}\:{a}_{\mathrm{0}} \:{and}\:{a}_{{n}} \\ $$

Question Number 38203 Answers: 0 Comments: 0

let x≠(π/2)+kπ,k∈Z.prove that (1/(2cosx)) =Σ_(n=0) ^∞ (−1)^n (cos(2n+1)x)

$${let}\:{x}\neq\frac{\pi}{\mathrm{2}}+{k}\pi,{k}\in{Z}.{prove}\:{that} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}{cosx}}\:=\sum_{{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{{n}} \left({cos}\left(\mathrm{2}{n}+\mathrm{1}\right){x}\right) \\ $$

Question Number 38202 Answers: 0 Comments: 1

find the value of ∫_0 ^1 e^(−x) (√(1−e^(−2x) ))dx

$${find}\:{the}\:{value}\:{of}\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{e}^{−{x}} \sqrt{\mathrm{1}−{e}^{−\mathrm{2}{x}} }{dx} \\ $$

Question Number 38201 Answers: 0 Comments: 0

calculate I = ∫_0 ^∞ xe^(−x^2 ) (√(1−e^(−2x^2 ) ))dx

$${calculate}\:{I}\:=\:\int_{\mathrm{0}} ^{\infty} \:\:\:{xe}^{−{x}^{\mathrm{2}} } \sqrt{\mathrm{1}−{e}^{−\mathrm{2}{x}^{\mathrm{2}} } }{dx} \\ $$

Question Number 38199 Answers: 1 Comments: 0

calculate ∫_0 ^1 ((√x)/(1+x^2 ))dx .

$${calculate}\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{\sqrt{{x}}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\:. \\ $$

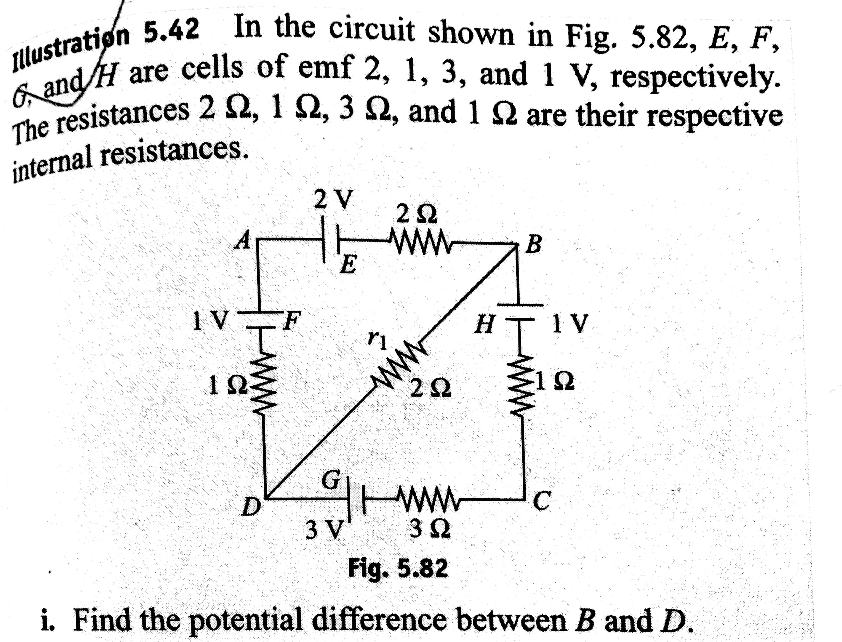
Question Number 38198 Answers: 0 Comments: 5

we give ∫_0 ^∞ e^(−x) ln(x)dx=−γ 1) calculate f(a)= ∫_0 ^∞ e^(−ax) ln(x)dx with a>0 2) let u_n = ∫_0 ^∞ e^(−nx) ln((x/n))dx find lim_(n→+∞) u_n

$${we}\:{give}\:\int_{\mathrm{0}} ^{\infty} \:\:{e}^{−{x}} {ln}\left({x}\right){dx}=−\gamma \\ $$$$\left.\mathrm{1}\right)\:{calculate}\:\:{f}\left({a}\right)=\:\int_{\mathrm{0}} ^{\infty} \:\:{e}^{−{ax}} {ln}\left({x}\right){dx}\:\:{with}\:{a}>\mathrm{0} \\ $$$$\left.\mathrm{2}\right)\:{let}\:{u}_{{n}} =\:\int_{\mathrm{0}} ^{\infty} \:\:{e}^{−{nx}} {ln}\left(\frac{{x}}{{n}}\right){dx}\:\:{find}\:{lim}_{{n}\rightarrow+\infty} \:{u}_{{n}} \\ $$

Question Number 38197 Answers: 0 Comments: 1

find a simple form of L(e^(−(√x)) ) L is laplace transform

$${find}\:{a}\:{simple}\:{form}\:{of}\:{L}\left({e}^{−\sqrt{{x}}} \right)\:\:{L}\:{is}\:{laplace}\:{transform} \\ $$

Question Number 38195 Answers: 0 Comments: 1

let x≥1 and δ(x)=Σ_(n=1) ^∞ (((−1)^n )/n^x ) 1) calculate δ(x) interms of ξ(x) if x>1 2)find δ(1) 3) find the value of Σ_(n=1) ^∞ (1/((2n+1)^2 )) 4) calculate δ(3) interms of ξ(3).

$${let}\:{x}\geqslant\mathrm{1}\:{and}\:\delta\left({x}\right)=\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}^{{x}} } \\ $$$$\left.\mathrm{1}\right)\:{calculate}\:\delta\left({x}\right)\:{interms}\:{of}\:\xi\left({x}\right)\:{if}\:{x}>\mathrm{1} \\ $$$$\left.\mathrm{2}\right){find}\:\:\delta\left(\mathrm{1}\right) \\ $$$$\left.\mathrm{3}\right)\:{find}\:{the}\:{value}\:{of}\:\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\left.\mathrm{4}\right)\:{calculate}\:\delta\left(\mathrm{3}\right)\:{interms}\:{of}\:\xi\left(\mathrm{3}\right). \\ $$

Question Number 38190 Answers: 1 Comments: 2

Question Number 38181 Answers: 2 Comments: 3

If y= x^((lnx)^(ln(lnx)) ) then (dy/dx) = ?

$$\mathrm{If}\:\mathrm{y}=\:\:{x}^{\left({lnx}\right)^{{ln}\left({lnx}\right)} } \:{then}\:\frac{{dy}}{{dx}}\:=\:? \\ $$

Question Number 38177 Answers: 0 Comments: 0

Question Number 38155 Answers: 0 Comments: 1

Propanol ,(C_3 H_7 OH) is an alcohol. a) State the functional group in propanol that makes it alcohol. b) Ethanol can be converted to a number of compounds as shown below. Ethene→ Ethane ↑ Ethylethanoate ⇆ Ethanol → Ethanoic acid ↓ soduimethanoate. when Soduim hydroxide solution reacts with Ethylethanoate ,Sodium Ethanoate and other products are obtained Give the name of the other products

Question Number 38154 Answers: 1 Comments: 0

Given that a,b,c are 3 consecutive term of a Geometric sequence f(n) , show that log a,logb,logc are the first 3 terms of an Arithmetic SequenceP(n).

$${Given}\:{that}\: \\ $$$$\:\:{a},{b},{c}\:{are}\:\mathrm{3}\:{consecutive}\:{term}\:{of}\: \\ $$$${a}\:{Geometric}\:{sequence}\:{f}\left({n}\right)\:,\:{show} \\ $$$${that}\:{log}\:{a},{logb},{logc}\:{are}\:{the}\:{first}\: \\ $$$$\mathrm{3}\:{terms}\:{of}\:{an}\:{Arithmetic}\:{SequenceP}\left({n}\right). \\ $$

Question Number 38151 Answers: 3 Comments: 8

a > b > 0 a^2 cos θ−b^2 sin θ=(a^2 −b^2 )sin θcos θ Find θ in terms of a, b. θ ∈ (0,(π/2)) .

$${a}\:>\:{b}\:>\:\mathrm{0} \\ $$$${a}^{\mathrm{2}} \mathrm{cos}\:\theta−{b}^{\mathrm{2}} \mathrm{sin}\:\theta=\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)\mathrm{sin}\:\theta\mathrm{cos}\:\theta \\ $$$${Find}\:\theta\:{in}\:{terms}\:{of}\:{a},\:{b}. \\ $$$$\:\:\theta\:\in\:\left(\mathrm{0},\frac{\pi}{\mathrm{2}}\right)\:. \\ $$

Question Number 38130 Answers: 4 Comments: 0

1. ∫tan^3 (2x)sec^5 (2x) dx 2. ∫_0 ^(π/3) tan^5 (x)sec^6 (x) dx 3. ∫tan^6 (ay) dy

$$\mathrm{1}.\:\int\mathrm{tan}^{\mathrm{3}} \left(\mathrm{2}{x}\right)\mathrm{sec}^{\mathrm{5}} \left(\mathrm{2}{x}\right)\:{dx}\: \\ $$$$\mathrm{2}.\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{3}}} \mathrm{tan}^{\mathrm{5}} \left({x}\right)\mathrm{sec}^{\mathrm{6}} \left({x}\right)\:{dx}\: \\ $$$$\mathrm{3}.\:\int\mathrm{tan}^{\mathrm{6}} \left({ay}\right)\:{dy}\: \\ $$

Question Number 38127 Answers: 0 Comments: 1

calculate ∫_0 ^∞ e^(−x) (√(1+e^(−2x) ))dx

$${calculate}\:\int_{\mathrm{0}} ^{\infty} \:\:{e}^{−{x}} \sqrt{\mathrm{1}+{e}^{−\mathrm{2}{x}} }{dx} \\ $$

Question Number 38126 Answers: 1 Comments: 2

calculate ∫_0 ^∞ e^(−2x) (√(1+e^(−4x) ))dx .

$${calculate}\:\:\:\int_{\mathrm{0}} ^{\infty} \:\:{e}^{−\mathrm{2}{x}} \sqrt{\mathrm{1}+{e}^{−\mathrm{4}{x}} }{dx}\:. \\ $$

Pg 1696 Pg 1697 Pg 1698 Pg 1699 Pg 1700 Pg 1701 Pg 1702 Pg 1703 Pg 1704 Pg 1705

Contact: info@tinkutara.com