Question and Answers Forum

AllQuestion and Answers: Page 170

Question Number 206248 Answers: 1 Comments: 0

∫(1/( (√((1−t)(2−t)))))dt=...?

$$\int\frac{\mathrm{1}}{\:\sqrt{\left(\mathrm{1}−{t}\right)\left(\mathrm{2}−{t}\right)}}{dt}=...? \\ $$

Question Number 206244 Answers: 1 Comments: 0

_1 : _2 = .... (A) 1 : (2)^(1/3) (B) (2)^(1/3) : 1 (C) 1 : (√2) (D) (√2) : 1 (E) 1 : (√3)

$$\:\: \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ _{\mathrm{1}} \::\: _{\mathrm{2}} \:=\:.... \\ $$$$\:\:\left({A}\right)\:\mathrm{1}\::\:\sqrt[{\mathrm{3}}]{\mathrm{2}}\:\:\:\:\left({B}\right)\:\sqrt[{\mathrm{3}}]{\mathrm{2}}\::\:\mathrm{1}\:\:\:\:\:\left({C}\right)\:\mathrm{1}\::\:\sqrt{\mathrm{2}} \\ $$$$\:\:\left({D}\right)\:\sqrt{\mathrm{2}}\::\:\mathrm{1}\:\:\:\:\left({E}\right)\:\mathrm{1}\::\:\sqrt{\mathrm{3}} \\ $$

Question Number 206232 Answers: 4 Comments: 0

Question Number 206230 Answers: 1 Comments: 0

Expand x^2 + 2x + 3 respect to x = −2. (a) (x − 2)^2 −2(x + 2) + 3 (b) (x + 2)^2 −2(x + 2) + 3 (c) (x + 2)^2 + 2(x + 2) + 3 (d) (x − 2)^2 −2(x − 2) − 3 is it taylors theorem?

$$\mathrm{Expand}\:\:\:\:{x}^{\mathrm{2}} \:+\:\mathrm{2}{x}\:+\:\mathrm{3}\:\:\:{respect}\:{to}\:{x}\:=\:−\mathrm{2}. \\ $$$$\left(\mathrm{a}\right)\:\left({x}\:−\:\mathrm{2}\right)^{\mathrm{2}} −\mathrm{2}\left({x}\:+\:\mathrm{2}\right)\:+\:\mathrm{3} \\ $$$$\left(\mathrm{b}\right)\:\left({x}\:+\:\mathrm{2}\right)^{\mathrm{2}} −\mathrm{2}\left({x}\:+\:\mathrm{2}\right)\:+\:\mathrm{3} \\ $$$$\left(\mathrm{c}\right)\:\left({x}\:+\:\mathrm{2}\right)^{\mathrm{2}} +\:\mathrm{2}\left({x}\:+\:\mathrm{2}\right)\:+\:\mathrm{3} \\ $$$$\left(\mathrm{d}\right)\:\left({x}\:−\:\mathrm{2}\right)^{\mathrm{2}} −\mathrm{2}\left({x}\:−\:\mathrm{2}\right)\:−\:\mathrm{3} \\ $$$$ \\ $$$$\mathrm{is}\:\mathrm{it}\:\mathrm{taylors}\:\mathrm{theorem}? \\ $$

Question Number 206227 Answers: 1 Comments: 0

OA=(4^x ) OB=_7 ^5 and AB=5 units

$${OA}=\left(\overset{{x}} {\mathrm{4}}\right)\:{OB}=_{\mathrm{7}} ^{\mathrm{5}} \:{and}\:{AB}=\mathrm{5}\:{units} \\ $$

Question Number 206224 Answers: 3 Comments: 0

find ∫_0 ^1 arctan(x^5 )dx

$${find}\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{arctan}\left({x}^{\mathrm{5}} \right){dx} \\ $$

Question Number 206212 Answers: 2 Comments: 4

Question Number 206216 Answers: 3 Comments: 0

Question Number 206198 Answers: 2 Comments: 0

Question Number 206200 Answers: 1 Comments: 0

∫((xsinx)/(1−cosx))dx

$$\int\frac{{xsinx}}{\mathrm{1}−{cosx}}{dx} \\ $$

Question Number 206178 Answers: 0 Comments: 3

Question Number 206177 Answers: 1 Comments: 0

Find total number of solutions of the equation sinx = logx.

$$\mathrm{Find}\:\mathrm{total}\:\mathrm{number}\:\mathrm{of}\:\mathrm{solutions}\:\mathrm{of} \\ $$$$\mathrm{the}\:\mathrm{equation}\:\mathrm{sin}{x}\:=\:\mathrm{log}{x}. \\ $$

Question Number 206171 Answers: 0 Comments: 0

Question Number 206168 Answers: 0 Comments: 1

Question Number 206160 Answers: 2 Comments: 1

If x and y are real numbers then is it possible that secθ = ((2xy)/(x^2 + y^2 )) ?

$$\mathrm{If}\:{x}\:\mathrm{and}\:{y}\:\mathrm{are}\:\mathrm{real}\:\mathrm{numbers}\:\mathrm{then}\:\mathrm{is}\:\mathrm{it} \\ $$$$\mathrm{possible}\:\mathrm{that}\:\mathrm{sec}\theta\:=\:\frac{\mathrm{2}{xy}}{{x}^{\mathrm{2}} \:+\:{y}^{\mathrm{2}} }\:? \\ $$

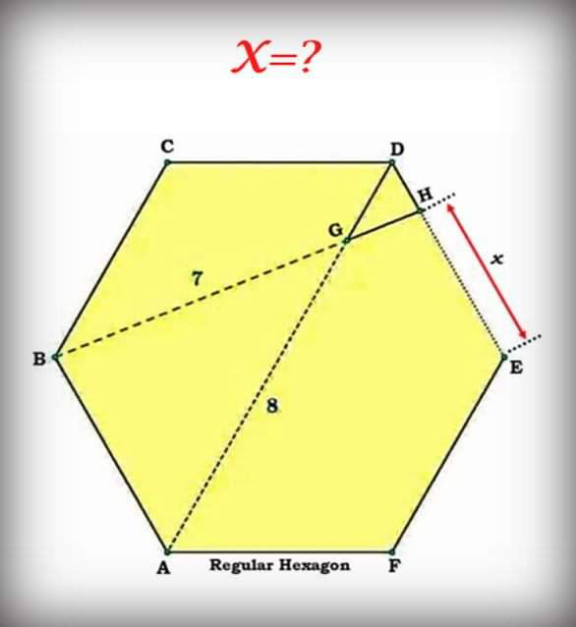
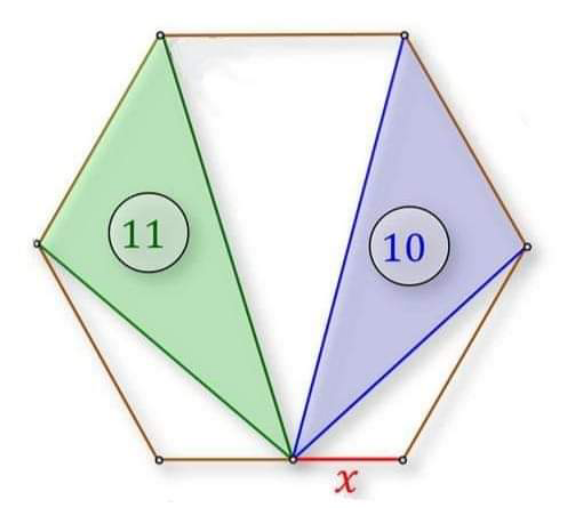
Question Number 206157 Answers: 2 Comments: 3

Question Number 206156 Answers: 1 Comments: 4

Question Number 206155 Answers: 4 Comments: 0

x = 2+(2/(2+(2/(2+(2/(2+(2/(2+(2/x))))))))) find x.

$$\:\:\:\:\mathrm{x}\:=\:\mathrm{2}+\frac{\mathrm{2}}{\mathrm{2}+\frac{\mathrm{2}}{\mathrm{2}+\frac{\mathrm{2}}{\mathrm{2}+\frac{\mathrm{2}}{\mathrm{2}+\frac{\mathrm{2}}{\mathrm{x}}}}}} \\ $$$$\:\:\:\mathrm{find}\:\mathrm{x}.\: \\ $$

Question Number 206150 Answers: 1 Comments: 0

Calcul ∣x−α∣ = ????? • x=−1 ; α ∈ [−1; −(3/4)] • x=2 ; α ∈ [0 ; 3] help please

$$\mathrm{Calcul}\:\:\:\mid\mathrm{x}−\alpha\mid\:=\:????? \\ $$$$\:\:\bullet\:\:\:\:\:\:\mathrm{x}=−\mathrm{1}\:\:;\:\:\:\alpha\:\in\:\left[−\mathrm{1};\:−\frac{\mathrm{3}}{\mathrm{4}}\right] \\ $$$$\:\:\bullet\:\:\:\:\mathrm{x}=\mathrm{2}\:\:;\:\:\:\:\alpha\:\in\:\left[\mathrm{0}\:;\:\mathrm{3}\right]\:\:\:\:\:\:\:\mathrm{help}\:\mathrm{please}\:\: \\ $$

Question Number 206151 Answers: 1 Comments: 0

Question Number 206146 Answers: 0 Comments: 0

Question Number 206142 Answers: 1 Comments: 0

let (d^2 y/dx^2 )+p(x)(dy/dx)+q(x)y=0 , x∈R where p(x) and q(x) are continuous function if y_1 = sinx−2cosx and y_2 = 2sinx +cosx are L.I (linearly independent) solution then ∣4p(0)+2q(1)∣ = ?

$$\:\:\:\:\mathrm{let}\:\:\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }+{p}\left({x}\right)\frac{{dy}}{{dx}}+{q}\left({x}\right){y}=\mathrm{0}\:,\:{x}\in\mathbb{R}\:\mathrm{where}\: \\ $$$$\:\:\:\:{p}\left({x}\right)\:\mathrm{and}\:{q}\left({x}\right)\:\mathrm{are}\:\mathrm{continuous}\:\mathrm{function}\:\mathrm{if} \\ $$$$\:\:\:\:{y}_{\mathrm{1}} =\:\mathrm{sin}{x}−\mathrm{2cos}{x}\:{and}\:{y}_{\mathrm{2}} \:=\:\mathrm{2sin}{x}\:+\mathrm{cos}{x} \\ $$$$\:\:\:\:\mathrm{are}\:{L}.{I}\:\left(\mathrm{linearly}\:\mathrm{independent}\right)\:\mathrm{solution} \\ $$$$\:\:\:\:\:\mathrm{then}\:\:\mid\mathrm{4}{p}\left(\mathrm{0}\right)+\mathrm{2}{q}\left(\mathrm{1}\right)\mid\:=\:?\:\:\: \\ $$

Question Number 206136 Answers: 1 Comments: 0

Question Number 206129 Answers: 1 Comments: 0

Question Number 206111 Answers: 3 Comments: 1

Question Number 206108 Answers: 3 Comments: 0

If x = (√(((√5) + 1)/( (√5) − 1))) then x^(12) = ?

$$\mathrm{If}\:{x}\:=\:\sqrt{\frac{\sqrt{\mathrm{5}}\:+\:\mathrm{1}}{\:\sqrt{\mathrm{5}}\:−\:\mathrm{1}}}\:\mathrm{then}\:{x}^{\mathrm{12}} \:=\:? \\ $$

Pg 165 Pg 166 Pg 167 Pg 168 Pg 169 Pg 170 Pg 171 Pg 172 Pg 173 Pg 174

Contact: info@tinkutara.com